이번에는 디지털논리회로이론 시간에 배우는 가장 기본적인 수의 체계에 대해서 배워볼 생각입니다.
십진법은 사람들이 수를 세고 표현하는 가장 기본적인 체계라고 할 수 있습니다.
사람의 손가락은 총 10개이기 때문에 손가락의 갯수를 기준으로 한 체계가 발전했다고 보고 있습니다.
그렇다면 저희가 배워야 할 수의 표현 방법에는 어떤 것이 있는지 본격적으로 알아보도록 하겠습니다.
저희는 총 4가지의 진법에 대해서 배울 것 인데, 2진법과 8진법 그리고 10진법과 16진법입니다.
| 2진법(Binary number) | 0, 1 |
| 8진법(Octal number) | 0 ~ 7 |
| 10진법(Decimal number) | 0 ~ 9 |
| 16진법(Hexadecimal number) | 0 ~ 9 이후 10부터 A 부터 F까지 6개의 문자로 표현 |
각각의 진법은 서로 다른 진법으로 변환할 수 있습니다.
그 예시로 2진법에서 8,10,16진법으로 변환할 수 있으며 다른 것 또한 마찬가지입니다.
그렇다면 여기서 가장 기본이 되는 2진법(Binary number)과 10진법(Decimal number)의 변환법에 대해서 배워보도록 하겠습니다.
- 2진법에서 10진법으로 변환 (Binary-to-Decimal Conversion)
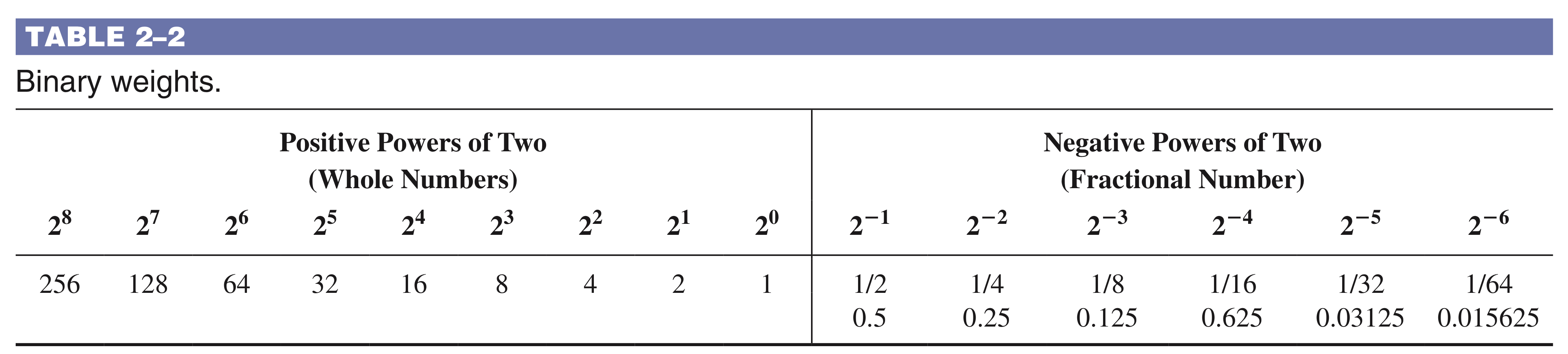
여기서 저희는 '가중치(weights)'라는 개념을 통해서 2진법을 10진법으로 변환할 수 있습니다.
위의 방식을 통해서 어떻게 2진법을 10진법으로 변환할 수 있는지 예시 문제와 함께 알아보도록 하겠습니다.
Ex ) 1101101을 10진법으로 변환하시오.
우리는 TABLE 2-2에 있는 가중치를 통해서 아래와 같이 10진법으로 변환할 수 있습니다.

위의 내용을 살펴보자면 Binary number의 '1'에 해당하는 자릿수(Weight)를 각각 뽑아내어,
뽑아낸 수들을 더하면 10진법으로 변환할 수 있습니다.
그렇다면 10진법을 2진법으로 바꾸는 것은 어떻게 할 수 있을까요?
- 10진법에서 2진법으로 변환 (Decimal-to-Binary Conversion)
제가 사용하는 교재의 경우 두 가지 방법에 대해서 알려주고 있습니다.
1. 가중치의 합을 통한 방법
2. 2로 계속해서 나누는 방법
2로 계속해서 나누는 방법에 대해서는 모두가 아시고 있을 것 이라고 생각합니다.
하지만 혹시 모르니 첫 번째 방법에 대해서 설명하고 난 이후에 설명해보도록 하겠습니다.
1. 가중치의 합을 통한 방법
말로만 하는 것은 이해하기 어려우니 예제 문제와 함께 솔루션을 통해서 알아보도록 하겠습니다.

위의 10진법을 가중치의 합을 통해서 2진법으로 바꾸는 방법은 무엇일까요?

이 방법과 같이 10진법을 2진법으로 변경할 수 있습니다.
위에서 가중치를 통해서 2진법을 10진법으로 변환한 방법을 거꾸로 한다고 보시면 됩니다.
첫 번째로, 10진법으로 표현된 것들을 2진법으로 표현할 수 숫자의 덧셈을 쪼갠다.
두 번째로, 쪼갠 숫자들을 2진법의 가중치에 맞는 자리에 '1'으로써 표현한다.
위의 두 가지 방법의 흐름을 통해서 10진법을 2진법으로 바꿀 수 있습니다.
2. 2로 계속해서 나누는 방법

2로 계속해서 나누는 방법은 모두가 아시듯이 10진법의 숫자를 2로 계속해서 나누는 것 입니다.
저희가 지금까지 배웠던 방식이지만 가시적으로 익숙한 모습은 아니기 때문에 익숙한 형태로
변환해보자면 아래와 같습니다.

이렇게 보면 저희가 익숙한 형태로써 충분히 이해하실 수 있으실 것이라고 생각합니다.
2로 계속해서 나누면서 나머지들을 화살표의 방향대로 읽으면 찾으실 수 있습니다.
지금까지 각 진법의 종류와 대표적인 2진법과 10진법 간 변환방법에 대해서 배워봤습니다.
저희는 디지털 시스템을 이해하기 위해서는 기본적인 'Binary Arithmetic'에 대해서 알아야 할 필요가 있습니다.
Binary Arithmetic은 아래 네 가지에 대해서 배워보도록 하겠습니다.
1. 덧셈
2. 뺄셈
3. 곱셈
4. 나눗셈
기본적인 산술이지만, 헷갈리는 부분이 있으니 잘 따라오시기를 바랍니다.
또한 문제와 풀이를 통해서 설명해보도록 하겠습니다.
- 덧셈 (Binary Addition)
덧셈에 대해서 배워보기 이전에 아래의 덧셈 룰에 대해서 아셔야 합니다.

여기서 "1 + 1 = 10"에 대해서 궁금하실 수 있는데요, 이는 저희가 아는 10진법의 10이 아니라 2진법에서 10(즉, 10진법으로 2)라는 것을 알고 가셔야 합니다. 나중에 뺄셈에서도 사용되니까 잘 알고 가셔야 합니다.


여기서 살펴보자면 두 가지 방법을 보실 수 있는데요, 첫 번째는 2진수 그 자체로 덧셈을 하는 것과 두 번째로 10진법으로 변환한 이후에
덧셈을 하고나서 2진법으로 다시 변환해주는 방법이 있습니다.
물론 선택은 여러분들의 선택이지만 저는 아직까지는 첫 번째 방법이 덜 번거러운 것 같아서 선호하는 것 같습니다.
여기까지 규칙과 더불어 보면 이해하기 쉬울 것이라고 생각합니다.
- 뺄셈 (Binary Substraction)



여기서도 마찬가지로 2진법에서 10진법으로 변환후에 계산하고, 다시 2진법으로 변환해줄 수 있습니다.
여기서 저는 예제문제를 보다가 헷갈리는 부분이 있었습니다. 바로 뺄셈에서 앞에 숫자를 꿔오는 것에 대해서 헷갈리는 부분이 있었습니다.
이 부분에 대해서 표현해보면 아래와 같습니다.

저는 처음에 이 문제가 헷갈렸던 것 같아요. 아무래도 바보같은 착각을 했던 것 같아요.
이 문제에 대해서 보자면 아래와 같습니다.

뺄셈을 하면서 바보같은 실수를 했다는 것을 알고, 찾아보고나서 알게 되었습니다.
위의 문제는 다른 곳에서 보고 작성했기 때문에 해당 주소에 가보시면 더 자세히 아실 수 있으실 것입니다.
주소는 맨 아래에 추가해놓을게요.
- 곱셈 (Binary Multiplication)
규칙

위의 규칙을 참고해서 아래의 문제를 보시면 됩니다.


이 역시도 문제의 해설과 함께보면 이해가 쉬우실 것이라고 생각합니다.
마찬가지로 10진법으로 보시고 나서 2진법으로 변환해서 생각해보실 수 있습니다.
위의 해설을 보시면 각 자릿수에 맞게 10진법의 곱셈과 똑같이 계산할 수 있다는 것을 보실 수 있으실거에요.
- 나눗셈(Binary Division)


위를 보면 10진법에서 나눗셈과 동일한 것을 알 수 있습니다.
나누고자 하는 2진수를 나눠지는 2진수의 크기에 따라서 0을 넣어주며 옆으로 칸을 넓혀갈 수 있습니다.
예를 들자면 아래와 같습니다.

어떻게 하시는지 이해가 가셨나요?
지금까지 각 진법과 더불어서 대표적인 2진법과 10진법 간의 상호 변환에 대해서 배웠고,
2진법의 산술법에 대해서 배웠습니다.
이는 기본적인 내용이니까 꼭 숙지하고 넘어가시기를 바랍니다.
마지막으로, 용어 하나를 짚고 넘어가야 할 것에 대해서 알려드리고 가겠습니다.
10진법에서 2진법으로 바꾸는 방법에서 10진법의 2로 계속해서 나누는 방법에 대해서 알려드리는 사진을 보시면 'MSB'와 'LSB'에 대해서 보실 수 있습니다.
1. MSB(Most Significant Bit) : 최상위 비트로 최상위의 값을 가지는 비트입니다.
2. LSB(Least Significant Bit) : 최하위 비트로 최하위의 값을 가지는 비트입니다.
다음에 공부를 하다보면 알 수 있지만, MSB와 LSB는 각각 또 다른 의미를 가지고 있습니다.
또 다른 의미에 대해서는 다음 시간에 한번 배워보도록 할게요.
부족한 글이지만 봐주셔서 감사합니다.
- 출처
- 2진수 뺄셈 참조 : https://eunhee-programming.tistory.com/66
'전자전기공학 > 디지털논리회로' 카테고리의 다른 글
| [Digital Logic #5][SOP/POS/Karnaugh Map] (2) | 2024.02.28 |
|---|---|
| [Digital Logic #4][부울대수(불대수)] (2) | 2024.02.27 |
| [Digital Logic #3][논리게이트(Logic Gate)] (0) | 2024.02.23 |
| [Digital Logic #2][보수와 부동소수 표현] (0) | 2024.02.20 |
| [Digital Logic #1-1][진법변환] (2) | 2024.02.19 |