디지털 시스템에서 음의 숫자를 표현하려면 어떻게 해야할까요?
1. 1's complement (1의 보수)
2. 2's complement( 2의 보수)
3. sign-magnitude
이렇게 총 세가지의 방법이 있습니다.
위의 세 가지 방법을 알기 전에 각 개념에 대해서 알아보도록 하겠습니다.
- 1's complement
1's complement의 경우 0과 1을 반대의 숫자로 뒤집어 주는 것으로 구해줄 수 있습니다.
Ex) binary number 10110010을 1's complement로 변환하면?
10110010 → 01001101
여기에서 추가적으로 디지털 회로에서 1's complement는 NOT Gate를 이용해서 구할 수 있습니다.

여기에서 추가적인 개념 하나 알고 가겠습니다.
· Unsigned number vs Signed number
Unsigned number : 음수가 아닌 수 즉, 양수와 영을 말한다.
Signed number: 양수, 음수, 영이 포함된다.
이 개념을 알고 가시는 것이 편할 것 이라고 생각합니다.
저희는 여기서 Signed number의 경우를 살펴볼 생각입니다.
1's complement의 범위는 어떻게 될까요?
$$ -(2^{N-1}-1) \;to\; (2^{N-1}-1) $$
위와 같은 방법으로 범위를 알 수 있습니다.
예를 들어보자면 8-bit의 범위는 아래와 같습니다.
$$ -(2^{8-1}-1) \; to \; (2^{8-1}-1) $$
으로 -127 ~ 127 범위인 것을 알 수 있다.
여기서 2가지 방식으로 +/- 0을 표현할 수 있다는 것을 알 수 있는데,
아래와 같이 표현할 수 있습니다.
00000000 (+0) , 11111111(-0)
- 2's complement
2's complement의 경우 binary number을 1's complement로 변환해준 이후에
1's complement의 LSB에 1을 더해주는 것으로 구할 수 있습니다.
아래 예시를 통해서 알아보겠습니다.
Ex) 10110010의 2's complement는?

여기서 2's complement를 구하는 또 다른 방법이 있습니다.
아래를 참고해서 보자면,

LSB인 맨 오른쪽부터 시작해서 1을 만나기 전까지 비트를 적습니다.
그 다음에 1을 만나면 1을 포함하여 그대로 적고난 이후에 나머지 왼쪽의 비트들은
1's complement로 바꿔주면 됩니다.

위는 음수의 2진수를 인버터와 덧셈기를 사용하여 구하는 방법에 대한 예시입니다.
범위는 아래와 같습니다.
$$ -(2^{N-1}) \;to\; (2^{N-1}-1) $$
하지만 여기서 1's complement와 다르게 오직 하나의 0만 가능합니다.
00000000 → 0
- Signed Binary Number
이제부터 본격적으로 부호가 있는 수에 대해서 배워보도록 하겠습니다.
1. Sign-Magnitude
부호가 있는 2진수가 부호-크기(Sign-Magnitude)로 표현될 때
가장 왼쪽에 있는 비트가 부호이고 나머지는 크기 비트들입니다.
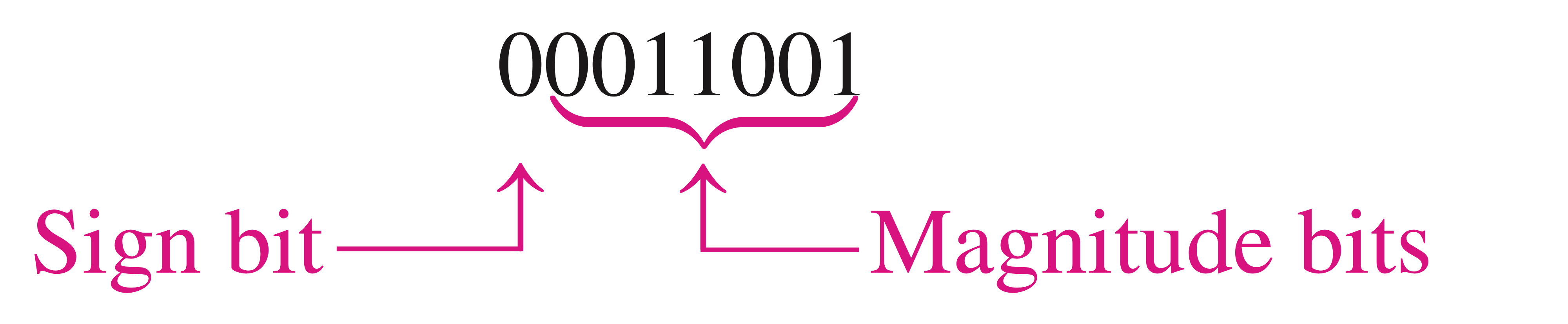
예를 들어서 위의 00011001은 10진법으로 25입니다.
이것을 -25로 표현하고 싶다면 10011001이라고 하면 됩니다.
2. 1's complement
1's complement의 경우 Sign-Magnitude와 같은 방식으로 양수를 표현합니다.
여기서 음수는 아래와 같이 표현합니다.
00011001(+25) → 11100110(-25)
즉, 1's complement에서 음수는 양수의 1's complement 보수입니다.
3. 2's complement
2's complement의 양수 역시 1's complement와 Sign-Magnitude와 같이 표현합니다.
여기서도 음수가 역시 다르겠죠?
00011001(+25) → 1100111(-25)
즉, 2's complement에서 음수는 양수의 2's complement 보수입니다.
정리하자면 양수의 binary number을 음수로 바꾸기 위해서 1's complement와
2's complement를 구해주면 되는 것이고, 또한 Sign-Magnitude를
이용한다고 보시면 됩니다.
이제는 부동소수에 대해서 배워보도록 하겠습니다.
- Floating-Point Numbers
"부동소수점 수"의 경우 매우 큰 수와 매우 작은 수를 표현할 때와 정수와 소수부 모두 가진 수 또한 표현할 수 있습니다.
여기서 부동소수의 경우 아래와 같이 세 가지 파트로 구성된 것을 알 수 있습니다.
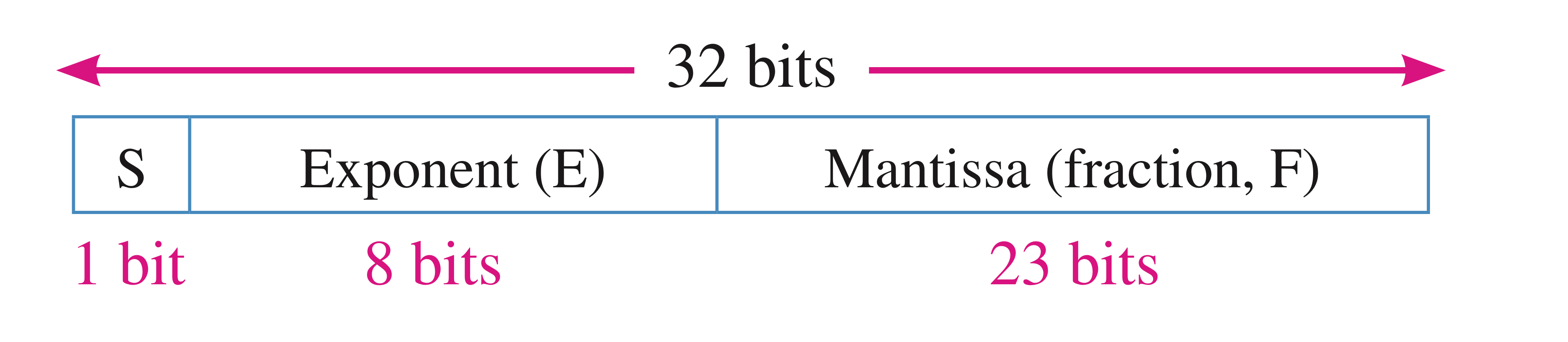
- 1. S : Sign(부호)
- 2. Exponent(E):
1. 지수는 실수의 크기를 표현합니다. 이진 부동 소수점에서는 보통 2의 지수를 사용합니다.
예를들어서 표현하자면 아래와 같습니다.
$$ 1011010010001\;=\;1.011010010001 * 2^{12} $$
지수 12는 127을 더하여 편향지수 139로 표현된다.
- 3. Mantissa(fraction, F)
가수는 실수의 소수 부분을 나타낸다. 즉, 정확한 값의 표현에 사용됩니다.
가수는 보통 부동 소수점 숫자에서 소수점 이하 부분을 정수로 표현한 것 입니다.
예를 들어서 0.75를 이진수로 표현하면 가수는 0.11입니다.
이를 구하는 방법은 2진수를 구하는 것과 같이 2로 계속해서 나누면 됩니다.
부동소수점 수 또한 말로하면 어렵기 때문에 문제와 솔루션을 함께 보면서 이해하도록 하겠습니다.


위의 문제와 함께 솔루션을 쫓아와 보시면 감이 잡히실 것이라고 생각합니다.
마지막으로, 가수에서 앞에서 부터 채워주고 난 이후에 모두 '0'으로 채워주는데
이는 일정한 형식을 유지하여 연산을 수행하기 위함이라고 합니다.
자세한 것은 IEEE 754 부동 소수점 표준을 통해서 알아볼 수 있습니다.
이 부분은 정말 어려운 부분이 맞는 것 같습니다.
이와 관련된 글은 위키피디아에서 참고했으며 아직은 많이 부족하다는 생각이 드네요.
아래 주소를 통해서 확인해보는 것이 좋을 것으로 생각이 됩니다.
https://ko.wikipedia.org/wiki/%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90
부동소수점 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 초기의 전기기계식 프로그래밍 가능한 컴퓨터 Z3에는 부동소수점 산술 기능이 포함되었다. (뮌헨의 국립 독일 박물관) 부동소수점(浮動小數點, floating point) 또
ko.wikipedia.org
다음에는 부호가 있는 수의 산술 연산과 더불어서 논리게이트에 대해서 배워보도록 하겠습니다.
감사합니다.
'전자전기공학 > 디지털논리회로' 카테고리의 다른 글
| [Digital Logic #5][SOP/POS/Karnaugh Map] (2) | 2024.02.28 |
|---|---|
| [Digital Logic #4][부울대수(불대수)] (2) | 2024.02.27 |
| [Digital Logic #3][논리게이트(Logic Gate)] (0) | 2024.02.23 |
| [Digital Logic #1-1][진법변환] (2) | 2024.02.19 |
| [Digital Logic #1][수의 표현(진법/변환/연산)] (2) | 2024.02.16 |