안녕하세요 이번에는 저번 포스팅에 이어서 SOP, POS 그리고 karnaugh Map에 대해서
알아보도록 할게요. 저번 포스팅이 궁금하시다면 아래에서 확인해 주세요.
2024.02.27 - [전자전기공학/디지털논리회로] - [Digital Logic #4][부울대수(불대수)]
[Digital Logic #4][부울대수(불대수)]
안녕하세요 오늘은 부울대수에 대해서 배워보도록 하겠습니다. 부울대수는 불대수라고도 부릅니다. 저는 부울대수라고 표현하도록 하겠습니다. 부울 대수에 대해서 알아보기 전에 부울대수에
monkey-engineer.tistory.com
이제 바로 SOP와 POS 그리고 Karaugh Map에 대해서 순차적으로 알아볼게요.
SOP(sum-of-products)
SOP는 문자들(변수 또는 변수의 보수)의 곱(부울의 곱셈)으로 구성되는 항입니다.
SOP의 예시는 아래와 같습니다.

여기에서 알고 넘어가야 할 것들이 있는데요,
SOP에서는 몇 개의 독립적인 '바'를 가질 수 있지만
몇 개의 변수가 공통'바'를 가질 수 없습니다.
$$ \overline{ABC} $$
위의 식은 불가능하지만 아래의 식은 가능합니다.
$$ \overline{A}\, \overline{B}\, \overline{C} $$
SOP에는 AND/OR과 NAND/NAND회로로 표현되며 두 회로는 등가입니다.


여기까지가 SOP의 기본이고 그렇게 어려울 것은 없을 것이라고 생각됩니다.
하지만 이제 '표준형 SOP'라는 것이 존재하는데요, 이것에 대해서 알아보도록 하겠습니다.
- 표준형 SOP(Standard SOP form)
표준 SOP식은 식의 각 곱항에 정의역의 모든 변수가 나타나는 식을 말합니다.
이 표준 SOP식은 나중에 카르노맵을 간략화 방법에서 매우 중요한 역할을 하게 됩니다.
그렇다면 일반 부울식에서 정의역은 무엇일까요?
일반 부울 식의 경우 정의역(Domain)은 보수 또는 비보수 형태로 식에 포함된 변수의 집합입니다.
$$ \overline{A}B\;+\;A\overline{B}C $$
위의 식의 경우 정의역은 변수 A, B, C의 집합인 것을 아시겠죠?
위의 식 또한 표준형 SOP이 아닌 것을 한 눈에 알 수 있는데요,
표준형 SOP로 바꾸는 방법은 부울 대수의 규칙6을 이용하는 것입니다.
규칙 6은 아래와 같습니다.
$$ (A\; + \; \overline{A} = 1)$$
이 규칙을 사용할 수 있는 이유는 보시는 바와 같이 결과적으로 '1'을
곱하는 것과 같기 때문입니다.
그렇다면 위의 식을 어떻게 표준형 SOP로 바꾸는지 한번 보겠습니다.
$$ \overline{A}B + A\overline{B}C \\ \leftrightarrow \; \overline{A}B(C+\overline{C})\; + \; A\overline{B}C \\ \leftrightarrow \; \overline{A}BC \; + \; \overline{A}B\overline{C} \; + \; A\overline{B}C$$
위의 방법에 대해서 읽어보신 이후에 바뀌는 과정을 보시면 이해하실 수 있습니다.
여기까지 SOP를 살펴봤으니 이제 POS를 살펴보겠습니다.
POS(product of sums)
POS는 문자들(변수 또는 변수의 보수)의 합(부울 덧셈)으로 구성되는 항입니다.
POS의 예시는 아래와 같습니다.


여기서도 SOP와 같이 '바'에 대한 제한이 있겠죠?
POS식에서 독립적인 '바'를 갖는 몇 개의 변수가 있을 수 있지만,
공통 '바'를 가질 수 없습니다.
$$ \overline{A}\; + \; \overline{B}\; + \; \overline{C}\;(O) \\ \overline{A\; + \;B\; + \; C} \; (X) $$
이제 SOP와 마찬가지로 표준 POS형을 만드는 방법을
예제와 솔루션을 통해서 알아보도록 하겠습니다.
사용되는 규칙은 부울대수 규칙8 입니다.
$$ (A\;*\; \overline{A} = 0) $$

여기서 부울대수 규칙8을 더해줄 수 있는 이유는 아실 것이라고 생각합니다.
SOP식과 POS식의 진리표로 변환
각 POS와 SOP식을 진리표로 변환하는 방법은 다음 두 가지를 기억해야 합니다.
1. SOP식은 곱항 중 적어도 하나의 항이 1이면, 1이 된다.
2. POS식은 합항 중 적어도 하나의 항이 0이면, 0이 된다.
이 두 가지를 기억하면서 아래의 문제와 솔루션을 함께 보시면 이해가 되실 거예요.
- SOP


- POS


이렇게 POS와 SOP를 진리표로 변경하면 쉽게 Logic Gate를 작성할 수 있습니다.
진리표를 통해서 이해를 하고. 회로를 디자인할 수 있기 때문에
진리표를 쉽게 작성할 수 있는 것이 가장 큰 힘이 될 것 같습니다.
이제 마지막으로 카르노 맵에 대해서 알아보고 추가적인 개념에 대해서 간단하게
훑어보고 나서 글을 마치도록 하겠습니다.
카르노맵(Karnaugh Map)
카르노맵은 부울표현식을 기계적으로 간단화하는 방법을 제시하는 것입니다.
카르노 맵은 진리표와 유사하지만 행과 열로 구성되어 있지 않고,
입력 변수의 2진수 값을 나타내는 셀(cell)들의 배열로 구성되어 있습니다.
카르노 맵에서 셀의 수는 진리표의 행의 수와 같을 뿐 아니라
입력 변수의 가능한 모든 조합의 수와 같습니다.
예를 들어서, 3변수일 경우 $$2^{3} = 8$$ 으로 8개 입니다.
이제 3변수와 4변수의 카르노 맵에 대해서 살펴보고 특징을 알아보도록 하겠습니다.
- 3변수 카르노맵

위는 3변수 카르노맵입니다.
변수가 A, B, C이기 때문에 총 8개의 셀이 있다는 것은 알고 있으실 겁니다.
위의 그림을 아래의 그림과 비교해서 살펴보면 SOP 카르노맵을 어떻게
작성할 수 있는지 알 수 있으실 거예요.


위의 왼쪽 사진의 결과값들이 SOP로 쓰여있다는 것을 볼 수 있으실 겁니다.
SOP 카르노맵과 POS 카르노 맵은 차이가 있는데요, 큰 차이는 아니지만 알고 계셔야 합니다.

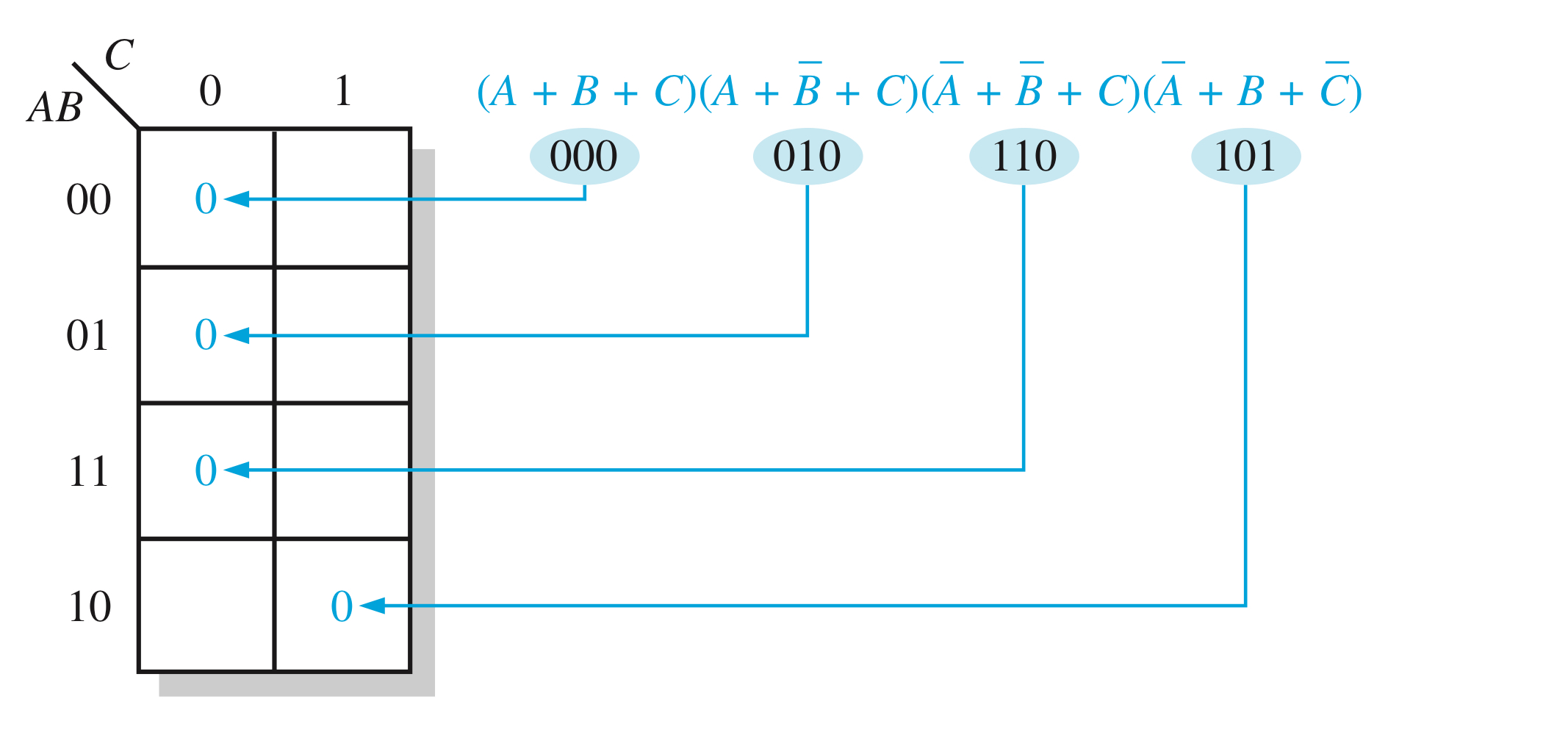
- 카르마맵 최소화
이제 하나 더 중요한 '그룹화'하여 변화하는 변수를 제거하여 조합논리를 단순화하는 방법에 대해서 배워보겠습니다.
아래에 예시 이미지와 함께 순서대로 쫓아와 보세요.

1. 왼쪽에 1을 두 개의 겹치는 그룹을 그룹화한다.
2. 경계를 넘어 변화하는 변수를 제거하여 각 그룹을 읽는다.
→ 우선 세로로 겹치는 영역은 B가 변화하며 가로로 겹치는 부분은 C가 변화합니다.
3. 세로로 겹치는 그룹은 $ \overline{A}\overline{C} $로 읽습니다.
4. 가로로 겹치는 그룹은 $ \overline{A}B $로 읽습니다.
위의 순서를 쫓아오다 보면 '그룹화'를 통해서 단순화 또는 최소화시킬 수 있습니다.
아래 또 다른 문제와 솔루션을 보면 감을 키울 수 있으실 거예요.


- 진리표를 카르마맵으로 표현
여기에서 진리표를 바로 카르마맵으로 표현할 수 있으며, 아래와 같습니다.

생각보다 별 것 없습니다. 위의 그림을 통해서 바로 이해가 가실거에요.
- 무정의(Don't care)
이제 카르마맵에 대해서 어느 정도 배웠는데요, 마지막으로 '무정의(don't care)'에
대해서 배워보도록 하겠습니다.
"일정 입력 변수 조합이 허용되지 않는 경우 이러한 허용되지 않는 상태는 발생하지 않는다."
라는 조건을 통해서 무정의 항을 '1' 또는 '0'으로 임의로 선택하여
가능한 그룹을 크게 만들 수 있습니다.
쉽게 말해서 무정의 항을 이용해서 카르노맵을 최소화 하는데에 유용하게 할 수 있는 것입니다.
글로만 봐서는 이해가 쉽지 않은 만큼 아래의 그림을 참고하시면 쉽습니다.

- 4변수 카르노맵

위는 4변수 카르노맵입니다.
4변수 카르노맵의 경우 3변수 카르노맵과 읽는 방법, 최소화, 무정의에 대해서
똑같기 때문에 아래부터 인접, 그리고 간단한 예제와 솔루션을 보고 끝내겠습니다.
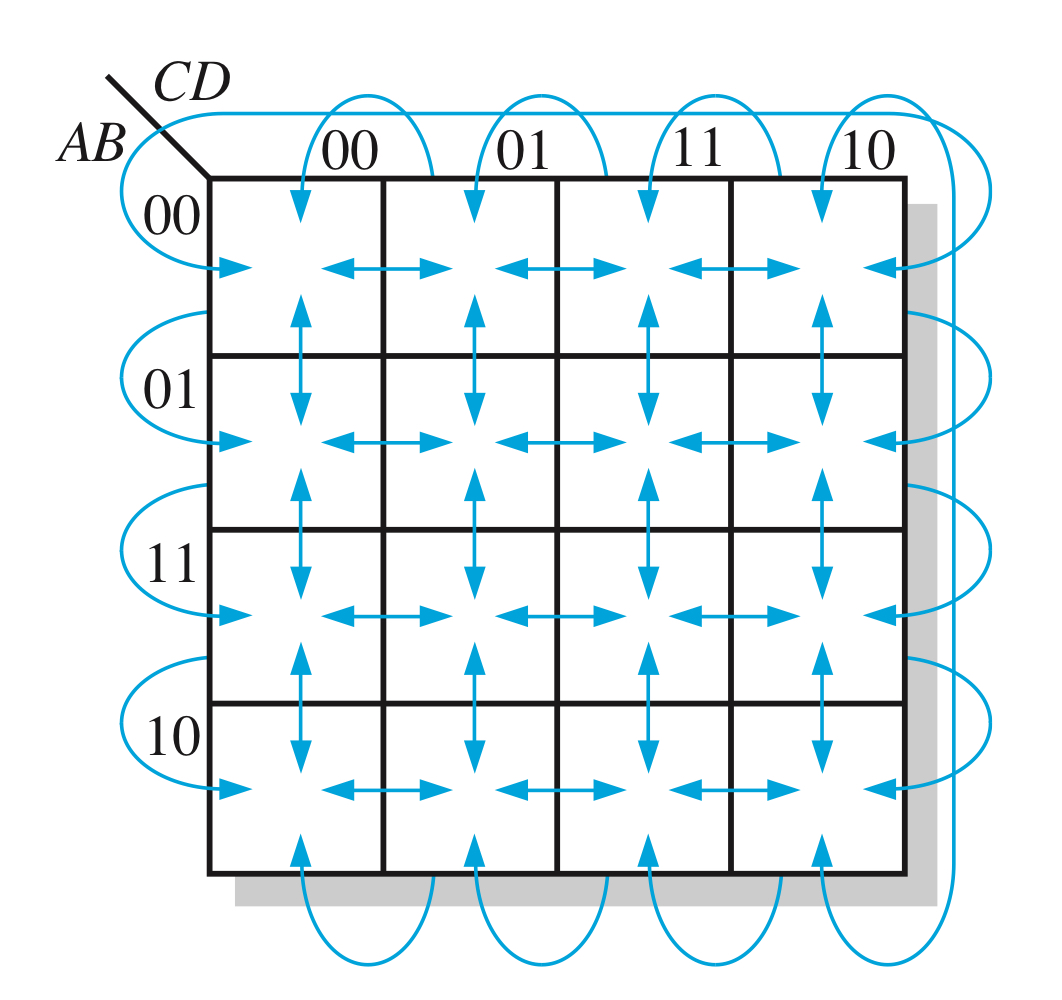
위의 그림은 인접의 방향에 대해서 표현한 것입니다. 이것을 보면 그룹화하는 것에 도움이 많이 될 거예요.
아래에는 간단한 문제와 이에 대한 솔루션입니다.


여기까지 카르노맵에 대해서 배워봤습니다.
만약 카르노맵에 대해서는 수정하거나 추가할 부분이 생기면
수정하거나 추가해서 글을 다시 올리도록 할게요.
이제 마지막으로 HDLs와 VHDL 그리고 Verilog에 대해서 알아볼게요.
- HDLs(Hardware Description Languages)
HDLs의 경우 설계한 회로를 PLD에 구현하기 위한 도구입니다.
HDLs에는 유명한 두 가지의 프로그래밍 언어가 있습니다.
1. VHDL(very high speed integrated circuit HDL)
2. Verilog
- VHDL
VHDL에서는 로직을 설명하는 세 가지 접근 방식이 있습니다.
1. Structural: Schematic과 같습니다.(components and block diagrams).
2. Dataflow: 부울 연산과 레지스터와 같은 등식입니다.
3. Behavioral: 시간 경과에 따른(상태 기계등) 사양입니다.
VHDL의 data flow 방식은 Boolean형 문을 사용합니다.
또한 기본 data flow 프로그램에는 두 부분이 있습니다.
1. Entity: entity부분은 I/O를 설명합니다.
2. Architecture: architecture부분은 logic부분을 설명합니다.
예를 들면 아래와 같습니다.

- Verilog
또 다른 표준 HDL은 Verilog입니다.
여기에서 I/O와 논리는 module이라는 하나의 단위로 설명됩니다.
또한 Verilog는 특정 기호를 통해서 Boolean 논리 연산자를 나타냅니다.
1. NOT : ~
2. AND : &
3. OR : |
그렇다면 Verilog로 OR gate를 작성하면 어떻게 될까요?
module OR_Gate (X, A, B);
input A, B;
output X;
Assign X = A | B;
endmodule
위와 같이 작성할 수 있습니다.
이제 여기까지 오늘 알아볼 내용이 다 끝났습니다.
HDLs은 아직 저도 제대로 공부해 본 적이 없이 때문에 완벽히 공부하면
추가적으로 올리도록 하겠습니다.
여기에 내용이 추가적으로 수정되어야 하거나 추가해야 하는 부분이
생긴다면 추후에 수정해 보도록 하겠습니다.
감사합니다.
'전자전기공학 > 디지털논리회로' 카테고리의 다른 글
| [Digital Logic #7][Functions of Combinational Logic/조합논리의 기능] (0) | 2024.03.01 |
|---|---|
| [Digital Logic #6][Combinational Logic Analysis/조합 논리의 해석] (3) | 2024.02.29 |
| [Digital Logic #4][부울대수(불대수)] (2) | 2024.02.27 |
| [Digital Logic #3][논리게이트(Logic Gate)] (0) | 2024.02.23 |
| [Digital Logic #2][보수와 부동소수 표현] (0) | 2024.02.20 |