· 목차
1. 기본적인 조합 논리회로
2. 조합 논리의 구현
3. NAND와 NOR게이트의 범용성
4. NAND와 NOR게이트를 사용한 조합 논리
5. 펄스 파형에 대한 논리회로 동작
안녕하세요. 지난 시간에는 SOP와 POS를 통해 조합 논리의 기본 형태에 대해서 구현했습니다.
또한 카르노맵(Karnaugh Map)을 통해서 체계적으로 부울 식을 간단화 하는 방법을 통해
가장 간략화된 SOP 및 POS를 얻는 방법에 대해서 배워봤습니다.
이에 대해서 궁금한 분은 아래의 글을 참고해주세요.
2024.02.28 - [전자전기공학/디지털논리회로] - [Digital Logic #5][SOP/POS/Karnaugh Map]
[Digital Logic #5][SOP/POS/Karnaugh Map]
안녕하세요 이번에는 저번 포스팅에 이어서 SOP, POS 그리고 karnaugh Map에 대해서 알아보도록 할게요. 저번 포스팅이 궁금하시다면 아래에서 확인해 주세요. 2024.02.27 - [전자전기공학/디지털논리회
monkey-engineer.tistory.com
이번에는 '조합 논리의 해석'에 대해서 알아보도록 할게요.
'조합 논리'란 규정된 입력 변수의 조합에 대해 규정된 출력이 나오도록
논리 게이트를 연결한 회로를 의미합니다.
또한 이 논리조합에는 저장 장치를 포함하지 않기 때문에 조합 논리회로의 출력 레벨은
항상 입력 레벨의 조합에 따라서 결정됩니다.
그렇다면 도대체 이 조합논리회로라는 것이 무엇인지 배워보도록 하겠습니다.
지난 시간에 SOP식은 각 곱항에 대해서는 AND Gate를 사용하며,
OR Gate를 사용하여 구현한다는 것을 배웠습니다.
여기에서는 AND-OR논리와 AND-OR-Invert논리에 대해서 배워보고
AND-OR논리의 한 형태인 배타적-OR 그리고 배타적-NOR에 대해서
배우고 난 이후에 NAND와 NOR게이트의 범용성에 대해서 살펴보며 마지막으로
펄스 파형에 대한 논리회로 동작을 살펴보고 마치도록 하겠습니다.
AND-OR 논리

AND-OR 게이트는 지난 시간에 말한 것 처럼 SOP를 구성하는 기본 구조입니다.
여기서 진리표를 살펴보자면 아래와 같습니다.

지난 포스팅 중에서 가능한 논리조합의 갯수는 $ 2^{N} $으로 구한다고 했던 것 기억하실겁니다.
여기서도 보면 총 16개의 논리 조합이 가능하다는 것을 보실 수 있습니다.
여기서 AND-OR 회로를 만들 수 있는데, 신기한 것은 Invert를 통해서 POS를
구현할 수 있다는 것 입니다.
AND-OR-Invert 논리


여기서 AND-OR 논리에 Invert를 추가하여 POS를 만드는 것에 대해서 보실 수 있습니다.
변형하는 과정에서 부울대수의 여러 규칙 및 법칙을 이용하시면 가능하다는 것을 저희는
지난 경험을 통해서 쉽게 알 수 있습니다.
두번째에서 식의 전개에 대해서 보실 수 있으니 천천히 부울대수의 규칙 및 법칙을 이용해서
쫓아가 보시면, 왜 이렇게 변화가 가능한지 알 수 있습니다.
1. $ AB\; + \; CD \;\;(SOP) $
2. $ \overline{\overline{\overline{AB}}\; + \; \overline{\overline{CD}}} \;\; (DeMorgan)$
3. $ \overline{\overline{(\overline{AB})(\overline{CD})}} \;\; (DeMorgan) $
4. $ (\overline{AB})(\overline{CD}) \;\; (Theorem3) $
이렇게 순서대로 보시면 이해가 확실히 가실겁니다.
지금까지 AND, OR, Invert를 가지고 SOP와 POS를 만들어 봤습니다.
이제 아래부터는 AND, OR, Invert를 응용하여 만드는
Exclusive-OR 논리와 Exclusive-NOR 논리에 대해서 배워보겠습니다.
배타적-OR 논리 (Exclusive-OR(XOR) Logic)

이 회로를 통해서 Exclusive-OR(XOR) 게이트를 구성할 수 있습니다.
지난 포스팅에서 배웠는데 혹시 까먹으셨을까봐 XOR 게이트와 진리표를 아래에 넣어놓을게요.


여기서 XOR은 $ X = A\oplus B $으로 표현하며,
$ X = A\overline{B}\;+\; \overline{A}B $ 입니다.
위에 응용한 방법이 쉽게 이해가 가시죠?
이제 Exclusive-NOR 논리에 대해서 살펴보겠습니다.
Exclusive-NOR(XNOR) 논리

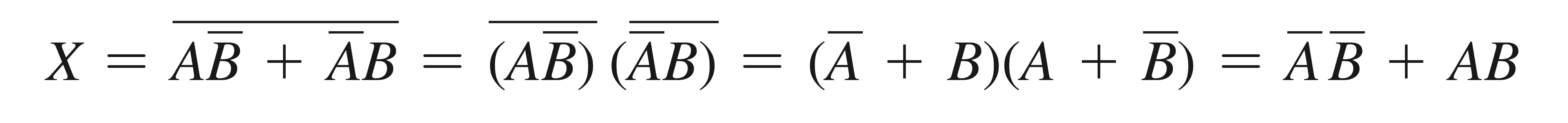
XNOR와 같은 경우 (a)와 같이 단순히 배타적-OR의 출력을 반전시켜서 구현되거나,
(b)와 같이 $ \overline{A} \overline{B} \; + \; AB $를 사용해서 직접 구현할 수도 있습니다.
XNOR의 진리표는 아래와 같습니다.

지금까지 기본적인 조합 논리회로를 살펴봤습니다.
이제는 부울식이나 진리표로부터 논리회로를
구현하는 방법에 대해서 살펴보도록 하겠습니다.
어떻게 보면 진리표나 부울식을 보고 회로를 구성한다는 것이
식이 적으면 간단하지만 식이 복잡하면 어렵기 때문에
이번에 확실히 알아두고 가는 것이 좋을 것 같습니다.
불 식으로부터 논리회로 구현하기
$$ X = AB + CDE $$
위의 식을 논리회로로 어떻게 구현할까요?

이 생각이 먼저 나셔야 합니다. 아마도 지난 포스팅을 보셨다면,
자연스럽게 생각이 나셨을 거라고 생각합니다.
또한 AND 연산보다는 OR 연산이 먼저 이뤄져야 한다는 것을
생각하셔야 합니다.

그렇다면 위의 회로를 바로 그려내실 수 있겠죠?
그렇다면 조금 복잡한 경우는 어떨까요? 아래의 식을 구현해보겠습니다.
$$ X = AB(C\overline{D} \; + \; EF) $$

위의 자료를 보고 아래와 같은 생각이 드셔야 합니다.
1. $\overline{D}$를 만들기 위한 Inverter
2. $ C\overline{D} $와 $ EF $를 만들기 위한 2개의 2-input AND Gate
3. $ C\overline{D} \; + \; EF$를 만들기 위한 1개의 2-input OR Gate
4. $X$를 만들기 위한 1개의 3-input AND Gate

위의 과정을 통해서 설계해보면 (a)와 같은 회로를 구성할 수 있습니다.
논리회로에서 각각의 논리회로를 거치는 동안 전파지연시간이 주요 고려사항일 때가 있습니다.
입력과 출력 사이에 게이트가 많을수록 전파지연시간은 더 길어지기 때문에
전체 전파지연시간을 줄이기 위해 SOP형태로 간략화 하는 것이 좋습니다.
위의 사항을 고려했을 때 (b)와 같은 SOP회로로 변환시킬 수 있습니다.
진리표로부터 논리회로를 구현하기
이번에는 진리표가 주어졌을 때 진리표를 통해서 SOP식을 작성하고,
논리회로를 구현할 수 있어야 합니다.

위의 진리표를 통해서 논리회로를 구현해보도록 하겠습니다.
우선 곱항에서 $\overline{A}BC$와 $A\overline{B}\overline{C}$을 OR하는 것으로
$X = \overline{A}BC \; + \; A\overline{B}\overline{C}$라는 SOP식을 구할 수 있습니다.
여기서 필요한 것들은 아래와 같습니다.
1. 3개의 변수를 곱할 AND가 필요하다.
2. $\overline{A}, \, \overline{B}, \, \overline{C}$를 만들기 위한 3개의 Inverter
3. 최종적인 형태로 만들 2-input OR Gate

위의 절차를 고려하며 회로를 작성하면 위와 같은 회로를 그리실 수 있습니다.
지금까지 부울식과 진리표를 통해서 회로를 작성하는 법에 대해서 배워봤습니다.
어떻게 보면 전파지연시간을 고려하며 SOP또는 POS 그리고
카르노맵을 통해서 식을 간단화하여 작성한다는 것이 핵심인 것 같습니다.
지금까지 포스팅을 통해서 배워온 것을 다 이용한다고 보시면 될 것 같습니다.
NAND와 NOR 게이트의 범용성
지금까지는 AND와 OR 그리고 Inverter 게이트를 통해서 구현된 조합회로를 살펴봤습니다.
이제는 NAND와 NOR게이트에 대해서 살펴볼것인데, 범용게이트라고 불리는 이유는
NAND 게이트를 가지고 Inverter, AND, OR, NOR게이트를 구현할 수 있습니다.
또한 NOR 게이트를 통해서도 Inverter, AND, OR 그리고 NAND를 구현할 수 있기 때문입니다.
여기서는 자료를 통해서만 살펴보도록 하겠습니다.
아마 자료를 자세히 살펴보는 것 만으로도 충분히 이해하실 수 있으실겁니다.
- 범용논리소자로서 NAND 게이트

- 범용논리소자로서 NOR 게이트

다음 내용을 배우기 위해서 알아둬야 할 내용이 있습니다.
지금까지 회로를 보면서 버블이 붙어 있다면 반전을 의미한다는 것이며,
여기서 2개의 연결된 버블은 이중 반전을 나타내어 서로 소거 된다는 것 또한 알 수 있습니다.
이제 NAND의 논리와 NOR의 논리에 대해서 배워보도록 하겠습니다.
- NAND Logic



여기서 참고하실 사항으로 NAND와 Negative-OR게이트는 같은 기능을 합니다.
1. SOP형태를 착안합니다.
2. 부울울대수로부터 이중반전이 소거된다는 것을 기억합니다.
3. 이중반전 버블을 더하면 NAND 게이트로 변할 수 있습니다.



바로 위에 버블캔슬과 NOR게이트 세 개로 만든것은 서로 등가입니다.
참고하실 사항으로 NOR 게이트와 Negative-AND게이트는 같은 기능을 합니다.
1. POS형태를 착안합니다.
2. 부울대수로부터 이중반전이 소거된다는 것을 기억합니다.
3. 이중반전 버블을 더하면 NOR게이트로 변할 수 있습니다.
이제 마지막으로 펄스 파형에 대한 논리회로 동작에 대해서 살펴보고 글을 마치도록 하겠습니다.
펄스 파형에 대한 논리회로 동작
펄스 파형에 대한 논리회로 동작에 대해서 어떻게 설명해야 할지에 대해서 많이 고민해봤습니다.
제가 생각했을 때에는 지난 포스팅에서 Waveform에 대해서 간단하게 보고 넘어갔기 때문에
예시 또는 문제와 솔루션을 보면 이해하기가 더 쉬울 것이라고 생각합니다.
아래 자료들을 자세히 살펴봐주세요.

위의 경우 입력 A, B, C가 인가되었을 때 출력파형 X를 보실 수 있습니다.
여기에서 Y는 B와 C가 인가된 OR 게이트라는 것을 아실 수 있습니다.
다음으로는 예제와 솔루션을 함께 볼게요.

문제는 A, B라는 입력파형이 있을 때 $G_{1},\; G_{2},\; G_{3}$에 대한 출력파형을 그리는 문제입니다.

마지막으로 $Y_{1},\; Y_{2},\; Y_{3},\; Y_{4},\;$에 해당하는 중간 출력파형과 이를 이용하여 X를
그리는 문제입니다. 입력파형은 솔루션에 나타나있습니다.

여기까지 목차에 해당하는 모든 내용을 훑어봤습니다.
솔직히 말해서 저 또한 말하는 감자이기 때문에
문제를 보고 머릿속에서 바로 착안한다는 것은
아직은 어렵다는 생각이 드네요.
하지만 계속해서 노력하다 보면 말하는 감자조차
계속해서 발전할 것이라고 믿으며 저 또한 계속해서
노력해 나가보도록 하겠습니다.
감사합니다.
'전자전기공학 > 디지털논리회로' 카테고리의 다른 글
| [Digital Logic #7-1][Function of Combinational Logic/조합논리의 기능] (0) | 2024.03.03 |
|---|---|
| [Digital Logic #7][Functions of Combinational Logic/조합논리의 기능] (0) | 2024.03.01 |
| [Digital Logic #5][SOP/POS/Karnaugh Map] (2) | 2024.02.28 |
| [Digital Logic #4][부울대수(불대수)] (2) | 2024.02.27 |
| [Digital Logic #3][논리게이트(Logic Gate)] (0) | 2024.02.23 |