Time Transformation은 주어진 신호를 시간의 변화에 따라 변환시키는 개념입니다.
시간 이동에는 Time Shifting, Time Reversal, Time Scaling이 있습니다.
그리고 마지막으로 위의 세 가지를 혼합해서 사용하는 Amplitude Transformation이 있습니다.
Time Shifing
$\text{x(t - a)}$는 $\text{x(t)}$를 time축상에서 오른쪽으로 a만큼 이동하는 것 입니다.
만약에 아래와 같이 그려지는 함수가 있다고 가정하고 그려보자면 아래와 같습니다.
$\text{x(t)} \; = \begin{matrix} 0 \; , \; t \leq -1 \\ t+1 \; , \; -1 < t \leq 0 \\ 1 \; , \; 0 < t \leq 2 \\ 0 \; , \; t > 2\end{matrix}$

위의 함수를 $\text{x(t-2)}$로 $\text{x(t)}$를 time 축상으로 오른쪽으로 a만큼 이동시키면 어떻게 될까요?
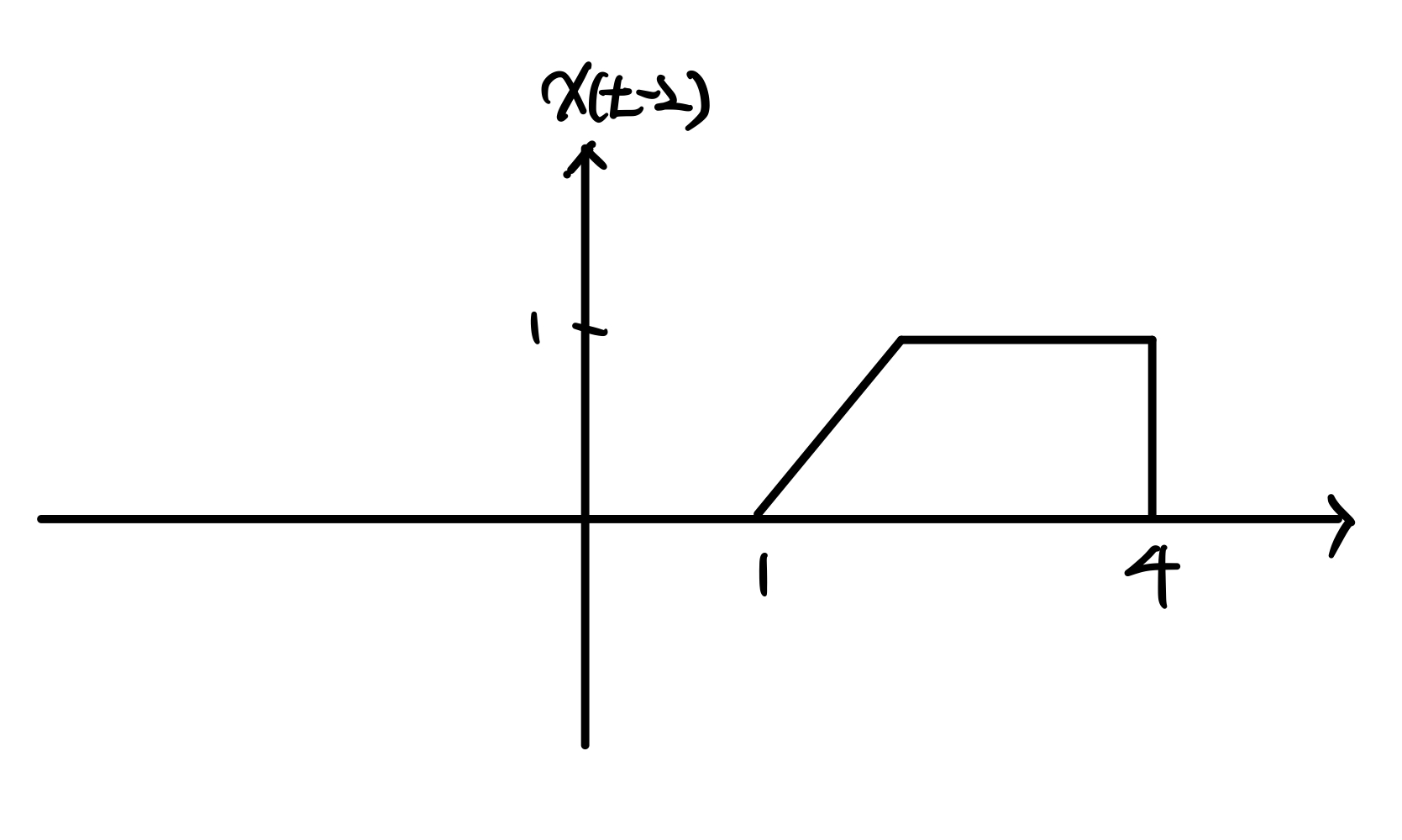
$\text{x(t)} \; = \begin{matrix} 0 \; , \; t \leq 1 \\ t-1 \; , \; 1 < t \leq 2 \\ 1 \; , \; 2 < t \leq 4 \\ 0 \; , \; t > 4\end{matrix}$
이 처럼 t축 상에서 오른쪽으로 이동한 구간이 나오게 되고, 맞춰서 그래프를 그려보면 아래와 같이 나오게 됩니다.
Time Reversal(= Time Reflection)
Time Reversal은 amplitude(t = 0)축에 대해서 반전시킨 것입니다.
$\text{x(t)} \; = \begin{matrix} 0 \; , \; t \leq -1 \\ t+1 \; , \; -1 < t \leq 0 \\ 1 \; , \; 0 < t \leq 2 \\ 0 \; , \; t > 2\end{matrix}$

여기서 그러진 함수를 $\text{x(-t)}$로 Time Reversal한다면,
아래와 같이 구간이 변경됩니다.
$\text{x(-t)} \; = \begin{matrix} 0 \; , \; t \geq 1 \\ -t+1 \; , \; 0 < t \leq 1 \\ 1 \; , \; -2 < t \leq 0 \\ 0 \; , \; t < -2\end{matrix}$

Time Scaling
Time Scaling은 넓이를 가로로 넓히거나 줄이는 형태의 그래프가 그려집니다.
여기서는 넓이가 넓어진 것은 expand이며, 넓이가 줄어든 것을 compress라고 합니다.
역시 마찬가지로 지금까지 기본형으로 설정해 놓은 아래의 그래프의 구간에서 시작하겠습니다.

이 구간은 위에서 계속 지켜보셨기 때문에 아신다는 생각으로 우선 compress 유형부터 보겠습니다.
$\text{x(2t)} \; = \begin{matrix} 0 \; , \; t \leq -\frac{1}{2} \\ 2t+1 \; , \; -\frac{1}{2} < t \leq 0 \\ 1 \; , \; 0 < t \leq 1 \\ 0 \; , \; t > 1 \end{matrix}$

이 다음으로, expand 유형은 아래와 같습니다.
$\text{x(0.5t)} \; = \begin{matrix} 0 \; , \; t \leq -2 \\ 0.5t+1 \; , \; -2 < t \leq 0 \\ 1 \; , \; 0 < t \leq 4 \\ 0 \; , \; t > 4 \end{matrix}$
결론적으로 위의 Time Scaling은
여기서 $\text{x(at)}$는 $\text{x(t)}$를 $\frac{1}{\vert a \vert}$배 Time Scaling된 것 이며,
$\vert a \vert > 1 \; \text{: compress}$ $\vert a \vert < 1 \; \text{: expand}$입니다.
여기서 세 가지 Time Transformation의 유형을 살펴봤습니다. 하지만, 여기에는 또 한가지 혼합형이 들어가게 됩니다.
혼합형은 Amplitude Transformation이라고 합니다.
Amplitude Transformation
Amplitude Transformation에 대해서는 다음 한 가지 주의 사항을 가지고 예제를 풀어보는 방식으로 알아보겠습니다.
주의해야할 사항은 Amplitude Transformation은 세 가지 유형의 순서가 중요하다는 것 입니다.
혼합형으로 변화하기 위해서는 첫 번째로 reflection 또는 scaling을 하고 난 이후에 마지막에 shifing을 해야한다는 것 입니다.
예제로 바로 알아보겠습니다.

위의 (a)에 대한 답은 아래와 같이 쉽게 그리실 수 있을겁니다.

(B)에서 간단한 shifting인 $\text{x(t-2)}$와 $\text{x(t+3)}$은 아래와 같이 그려집니다.
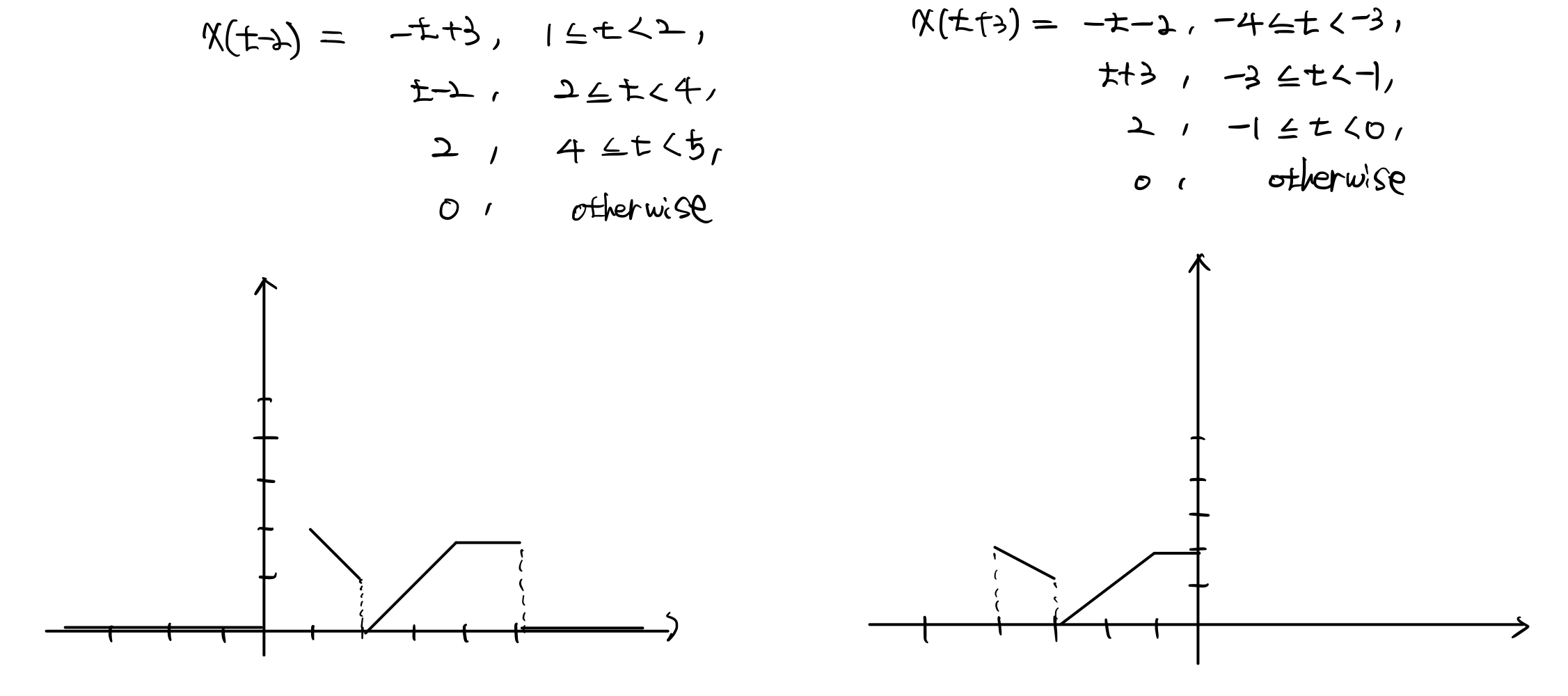
이건 위에서 배워봤으니 쉽게 예상하실 수 있지만, 이제 $\text{-3t-2}$는 혼합형이기 때문에 복잡하기 때문에 아래의 그림의
순서를 쫓아오시고, 제가 말한 주의사항을 유의하면서 보시면 쉽습니다.

여기서 마지막 과정은 -3으로 묶어서 그렇지만 $\text{x(-3t-2)}$라는 것을 알 수 있습니다.
이제 $\text{x(-3t-2)}$의 과정을 단계별로 봤으니, $\frac{2}{3} t + \frac{1}{2}$는 한번에 묶고나서
제가 말한 유의사항을 생각하면서 그리면 한번에 그리면 더 빠르게 할 수 있습니다.
이것을 묶으면 $x(\frac{3}{2}(t+\frac{3}{4}))$이 되고, 우선 scaling을 진행하고 나서 shifting을 수행하면 됩니다.

지금까지 Time Transformation을 알아봤습니다.
글 읽어주셔서 감사합니다.
'전자전기공학 > 신호와시스템' 카테고리의 다른 글
| [신호와 시스템][Elementary Signals] (8) | 2024.11.12 |
|---|---|
| [신호와 시스템][Energy and Power signal] (0) | 2024.11.04 |
| [신호와 시스템][Periodic & Aperiodic signal] (6) | 2024.10.06 |