오늘은 Energy signal과 Power signal에 대해서 배워보도록 하겠습니다.
Energy signal과 Power signal을 이용하는 이유는 무엇일까요?
Energy signal은 무한한 시간 동안 에너지가 유한한 신호입니다. 쉽게 이야기해서 신호이 전체 에너지가
(대부분의 경우) 유한한 경우를 말합니다. 그 예시로 펄스 등과 같이 비주기적인 신호가 에너지 신호에 해당합니다.
Power signal은 무한한 시간 동안 평균 전력이 유한한 신호입니다. 주기적인 신호나 지속적인 신호에서
전력을 구하는 것으로 전력이 유한하지만 에너지는 무한한 신호입니다.
예시로 사인파 등과 같은 주기적인 신호가 전력 신호에 해당하게 됩니다.
Energy signal과 Power signal을 판별하는 방법은 아래의 수식을 이용하는 것 입니다.
$\text{E} \; = \; \lim\limits_{L\to \infty} \; \int_{-L}^{L} \left\vert x(t) \right\vert^{2} \; dt \; = \int_{-\infty}^{\infty} \left\vert x(t) \right\vert^{2} \; dt$
위의 결과값이 $0 \; < \; \text{E} \; < \; \infty$이고, $\text{P} \; = \; 0$이라면 Energy 신호입니다.
$\text{P} \; = \; \lim\limits_{L \to \infty} \left[ \frac{1}{2L} \int_{-L}^{L} \left\vert x(t) \right\vert^{2} \; dt \right] \; = \; \lim\limits_{L \to \infty} \left[ \frac{1}{2L}E \right]$
위의 수식을 변형시키면, $\text{E} \; = \; \lim \limits_{L \to \infty} \left[ 2L \right] \; P$라는 수식이 됩니다.
위의 수식을 이용하면 E 또는 P 중에서 하나를 구하면 나머지 하나는 쉽게 구할 수 있습니다.
여기서도 마찬가지로 결과값이 $0 \; < \; \text{P} \; < \; \infty$이고, $\text{E} \; = \; \infty$이라면 Power 신호입니다.
여기서 주기(periodic sinal) 신호라면 위의 Power signal이 주기 T인 구간 내에서는 어느 구간에서도 같을 것 입니다.
구간 2L이 주기의 정수배가 되도록 극한값을 취하면 2L인 구간에서 $\text{x{t}}$의 총 에너지는 한 주기에 대한 에너지의
$\text{m}$배가 되어 아래의 증명과정의 최정 결과인 $\text{P} \; = \; \frac{1}{T} \int_{0}^{T} \left\vert x(t) \right\vert \; dt$가 됩니다.

위의 주기 신호 공식을 적용할 수 있는 $\text{x(t)} \; = \; \text{A}sin(w_{0}t + \phi)$의 정현파 신호를 예제로 풀자면,
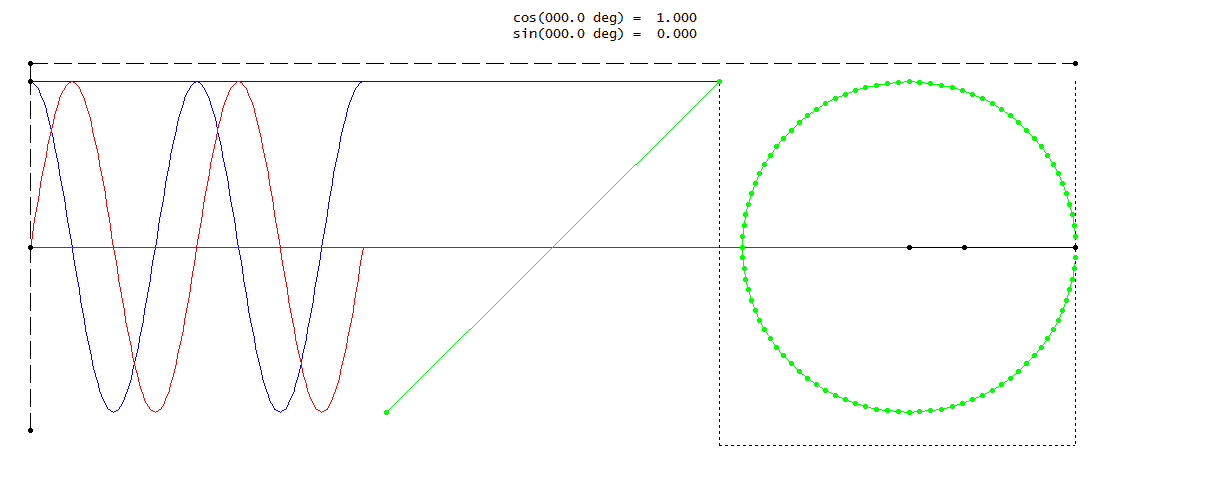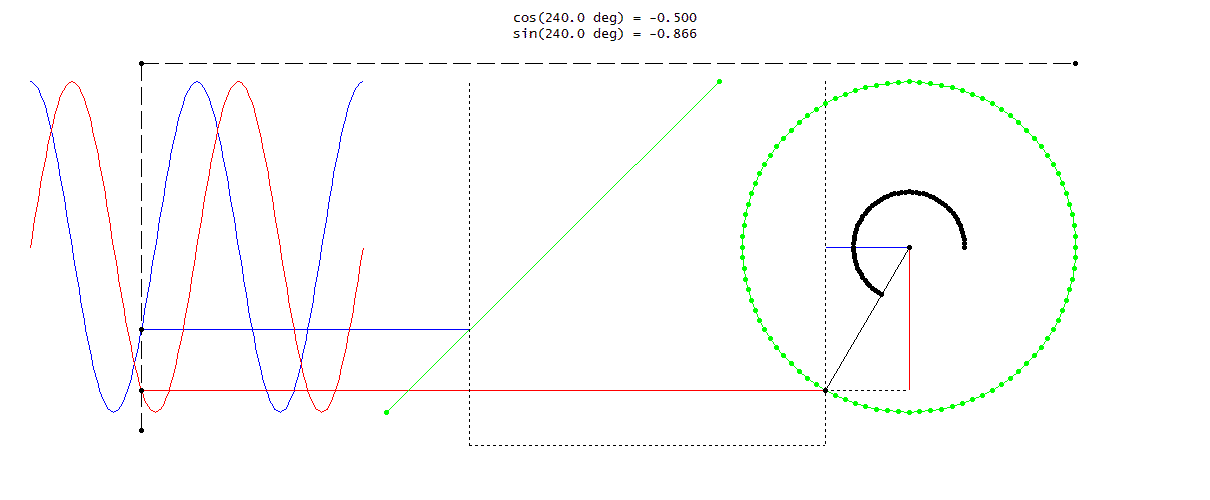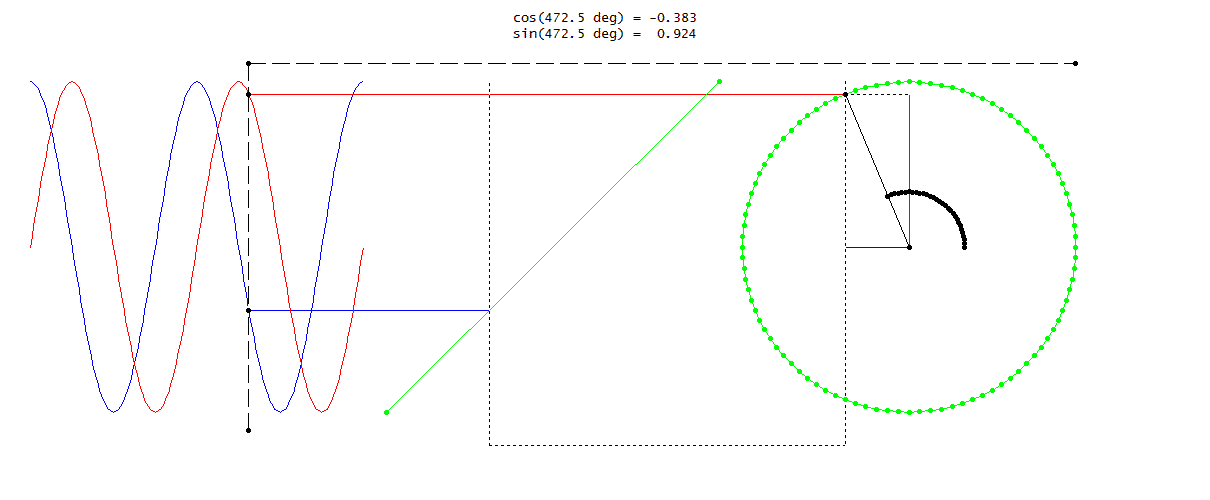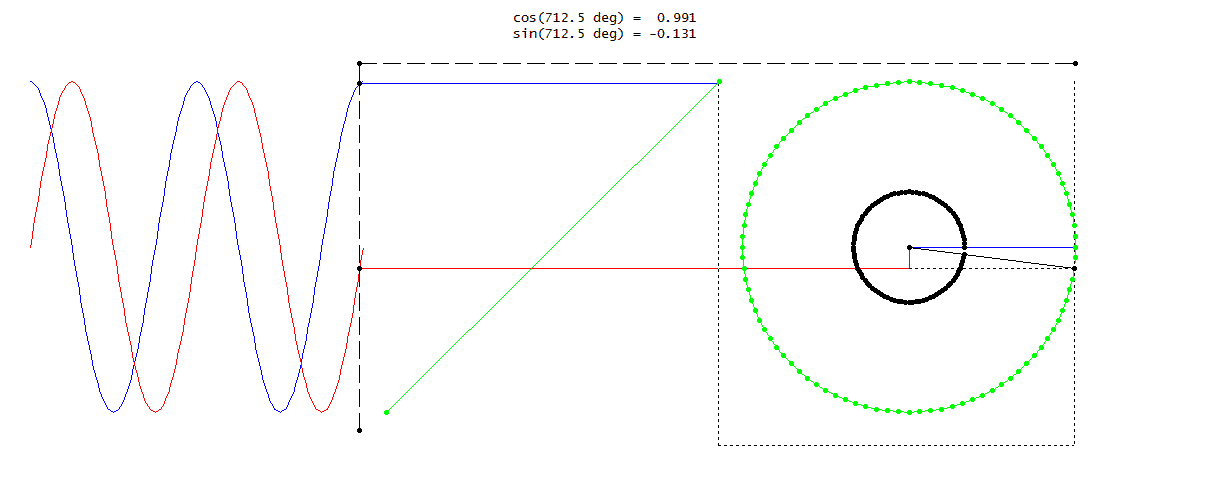

$T \; = \; \frac{2\pi}{w_{0}}$
$P \; = \; \frac{1}{T} \ int_{0}^{T} A^{2}sin^{2}(w_{0}t + \phi) \; dt$
$ P\; = \; \frac{A^{2}w_{0}}{2 \pi} \int_{0}^{\frac{2 \pi}{w_{0}}} \left[ \frac{1}{2} - \frac{1}{2}cos(2w_{0}t + 2\phi) \right] \; dt$
$= \; \frac{A^{2}}{2}$
이런 과정을 통해서 주기 신호를 풀어낼 수 있습니다.
그렇다면 비주기 신호는 어떨까요?
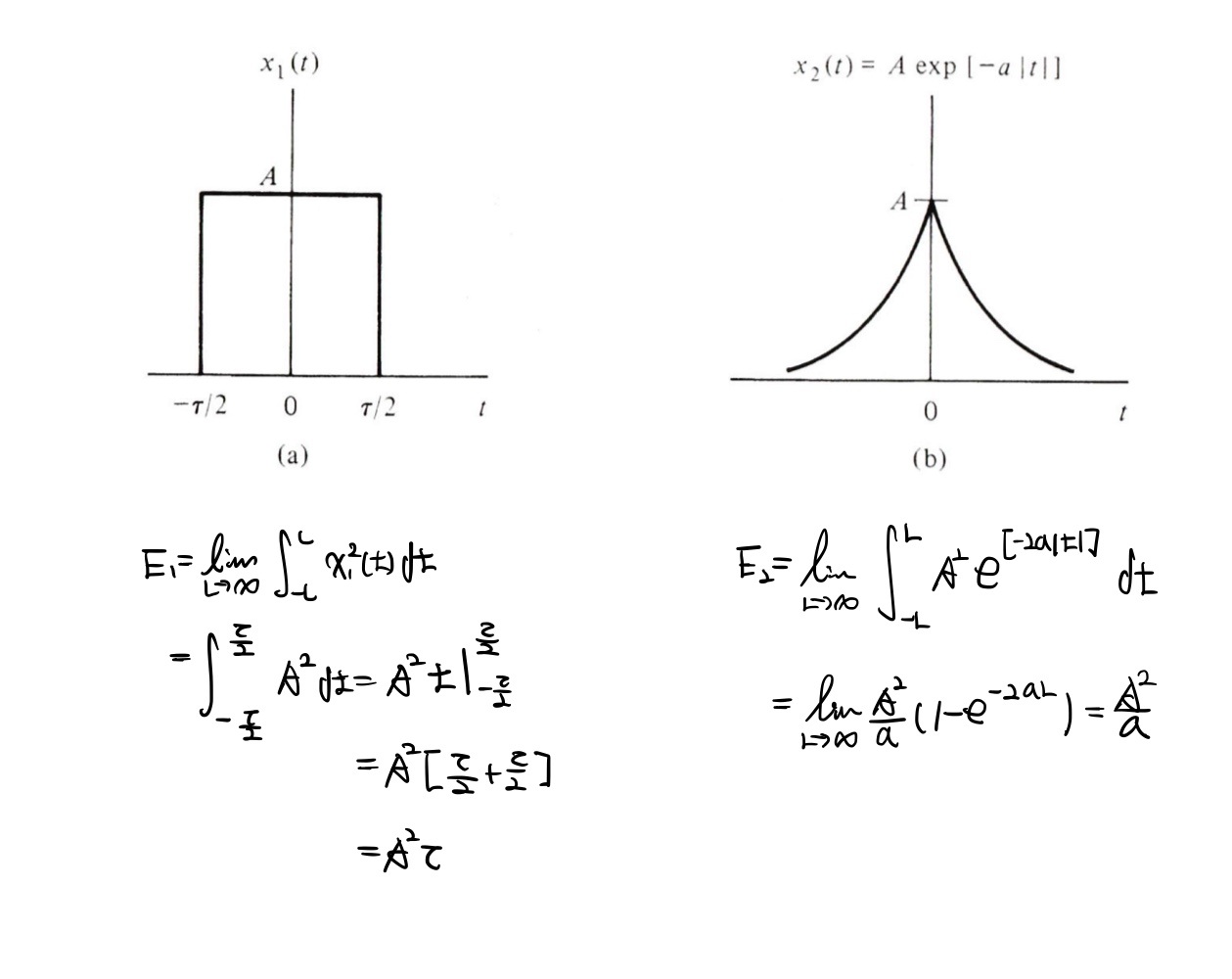
위의 두 신호에서 왼쪽은 $\frac{-\tau}{2}$와 $\frac{\tau}{2}$의 바깥 영역은 모두 '0'으로 Strictly time limited하다고 표현하며
오른쪽 처럼 t가 오른쪽 또는 왼쪽으로 갈수록 0으로 수렴하는 신호를 asymptotically time limited라고 표현합니다.
물론 예외는 존재하지만 왼쪽도 유한한 신호를 가지고 오른쪽도 0으로 수렴하기 때문에 에너지 신호가 됩니다.
지금까지 Energy signal 인지 Power signal인지 구분하는 방법과 Energy signal에서
strictly time limited한 표현과 asymptotically time limited한 표현에 대해서 배워봤고,
다음에는 time transformation에 대해서 배워보도록 하겠습니다.
글 읽어 주셔서 감사합니다.
'전자전기공학 > 신호와시스템' 카테고리의 다른 글
| [신호와 시스템][Time Transformation] (2) | 2024.11.14 |
|---|---|
| [신호와 시스템][Elementary Signals] (8) | 2024.11.12 |
| [신호와 시스템][Periodic & Aperiodic signal] (6) | 2024.10.06 |