이전 시간에는 cache의 대략적인 구조인 Direct mapped cache와 n-way set associative에 대해서 배웠었습니다.
간략하게 살펴봤기 때문에 자세한 부분을 더 다뤄야 겠다는 생각으로 다시 글을 작성해보려고 합니다.
이전의 포스팅을 보고 전체적인 부분을 둘러보시고 이 포스팅을 보시면 이해하기가 쉬우실 거라고 생각합니다.
cache에는 Direct mapped / n-way set associative / fully associative cache가 있습니다.
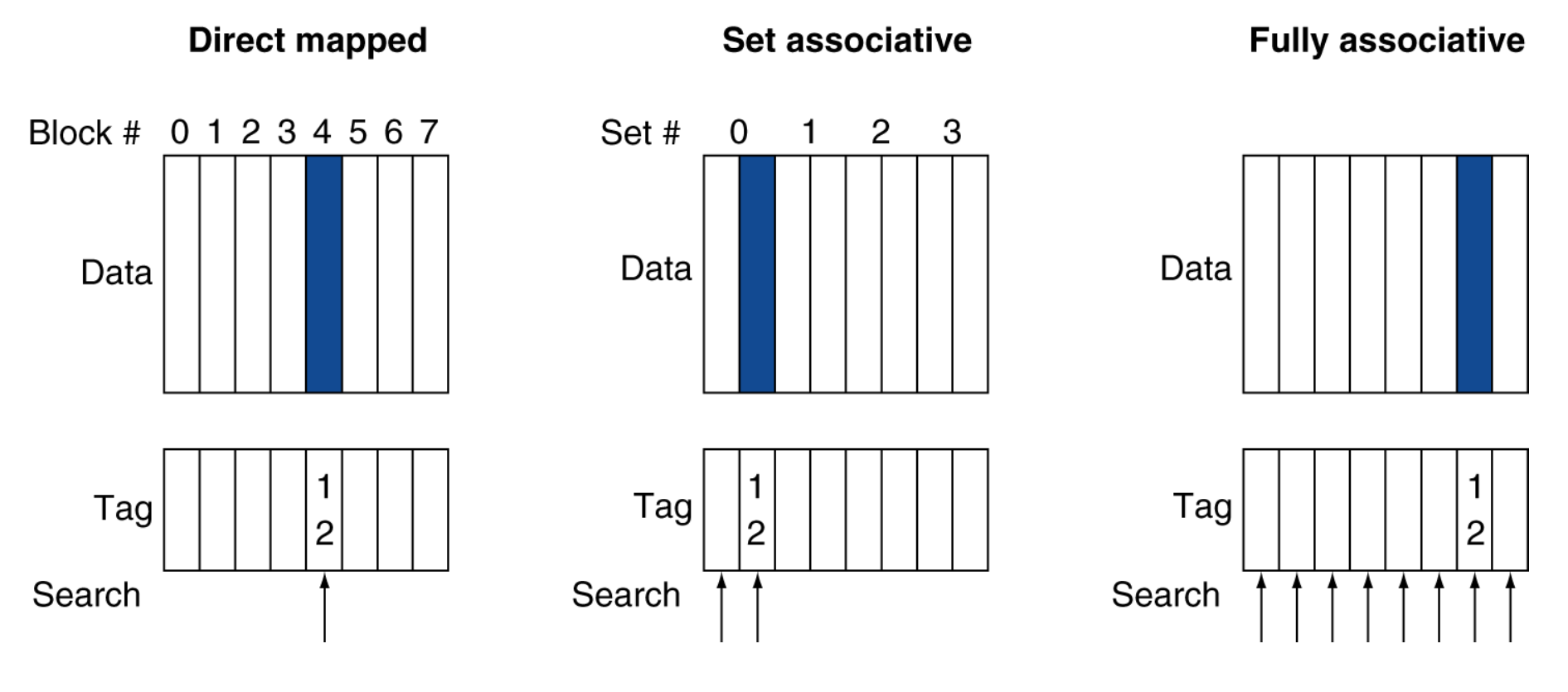
이전 시간에 이야기 했던 것 처럼 Hard Disk 또는 RAM은 접근(Access)속도가 느리기 때문에 cache를 사용합니다.
간략한 예로, CPU의 구조를 배울 때, Instruction 및 Data memory는 cache memory로 구성됩니다.
그렇다면 각 cache memory의 형태에 따른 문제를 어떻게 접근하고 각자 어떤 장단점이 존재하게 될까요?
Direct mapped
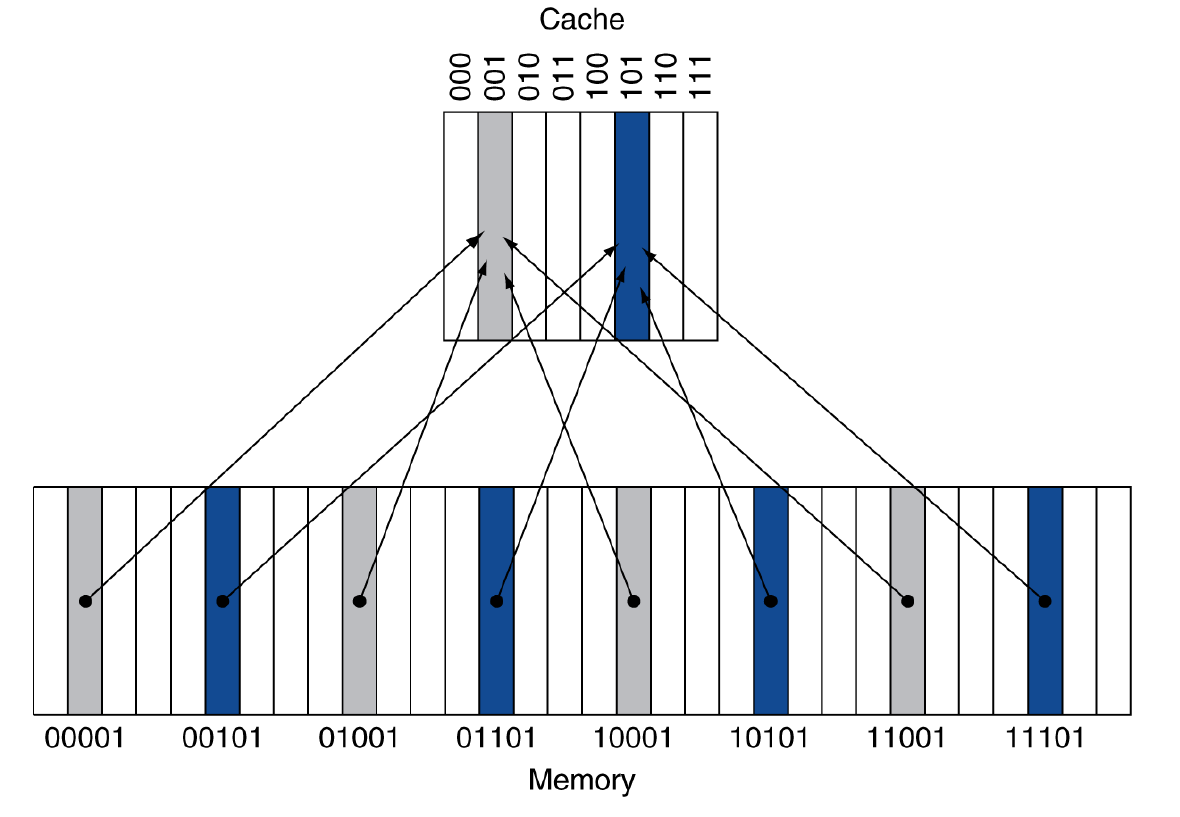
Direct mapped cahce는 cache를 mapping하는 가장 기본적인 방법입니다.

memory에서 cache를 가지고 와서 mapping할 때 저희는 Tag와 block index를 가지고 cache hit와 miss를 판별하게 됩니다.

여기서 cache hit와 miss를 어떻게 구별할 수 있을까요?
아래 문제를 풀어보면서 감을 잡아보도록 하겠습니다.
cache의 spec이 Cache size = 64Byte, word = 4 Byte, Block = 4 Byte, 입력 주소가 8bit일 때 아래의 표를 채워보자.
| Cache category | Tag | Block index | Block offset | Byte offset |
| Direct mapped | ||||
| 2-way set associative | ||||
| fully associative |
1. $\text{Block index =} \; \frac{Cache size}{word * Block} \; = \; \frac{64Byte}{16Byte} \; = \; \text{4 Blocks} \; = \; 2^{2}\; = \; \text{2 bit}$
2. $\text{Block offest =} \; \text{block} \; = \; \text{4Byte} \; = \; 2^{2} \; = \text{2 bit}$
3. $\text{Byte offset =} \; 2^{2} \; = \; \text{2 bit}$
구해놓은 bit를 가지고 위의 address 구조를 통해서 Tag를 구하면 아래와 같습니다.
입력 주소 8bit, Block index 2bit, Block offset 2bit, Byte offset 2bit 그러므로 Tag는 2bit이 됩니다.
Tag는 입력주소 - Block index - Block offset - Byte offset이 됩니다.
| Cache category | Tag | Block index | Block offset | Byte offset |
| Direct mapped | 2bit | 2bit | 2bit | 2bit |
2-way associative

위의 문제를 2-way associate로 풀기 위해서는 해당 그림을 이해해야 합니다.
만약 8개의 Block index를 가지고 있는 Direct mapped cache의 구조라면 2-way set associative로 바꿨을 때,
오른쪽과 같이 set(block index/n-way의 숫자)구조를 가지게 됩니다.
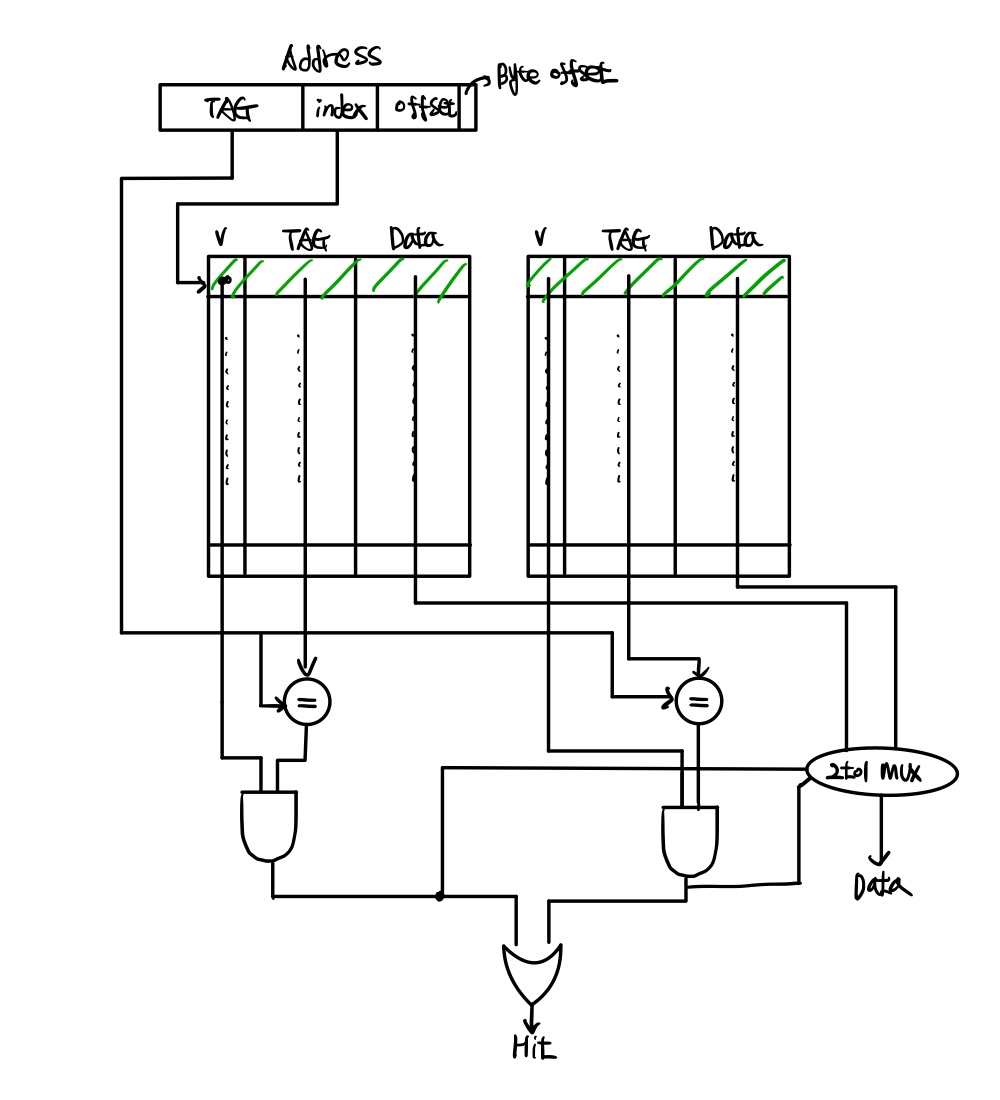
만약에 그림과 같이 변경하게 된다면 8개의 block index가 반으로 줄어들게 되고, block offset이 더 늘어나게 되겠죠?

위의 구조로 이해를 해보자면, 2-way set associative일 때 Block은 n으로 나눈 숫자가 되고,
Block(또는 line)의 길이라고 할 수 있는 Data(word)의 길이는 더 길어지게 됩니다.
왜냐하면, 위의 이미지처럼 Tag와 Data의 길이가 n배가 되기 때문입니다.
여기서 물리적인 면적을 보자는 것이지 실제로 block offset의 bit가 더 늘어난다고 생각하시면 안됩니다.
block offset은 캐시 블록 내에서 특정 데이터를 찾기 위한 위치를 가르키는 것 입니다.
block 내부의 word단위의 크기는 바뀌지 않기 때문이라고 생각하시면 될 것 같습니다.
쉽게 이야기하자면, n-way set associative라고 한다면 "n배로 가로 옆으로 뚱뚱해지고, 나누기 n을 한 만큼 키는 작아진다."
라고 이해하시면 앞으로 bit수를 구할 때 쉬울 것 같다는 생각이 듭니다.
결국 위에서 문제를 다시 2-way set associative에 적용해보자면 아래와 같이 표를 채울 수 있을 것 같습니다.
| Cache category | Tag | Block index | Block offset | Byte offset |
| 2-way set associative | 3bit | 1bit | 2bit | 2bit |
Fully associative
Fully associative는 어느 Block에나 저장될 수 있습니다. 매우 유연하지만 하드웨어 구현이 복잡하고 탐색 비용이 크게 됩니다.
탐색 비용이 크다는 것은 모든 Block을 비교기를 이용해서 비교하기 때문에 탐색 비용이 커지는 것 입니다.
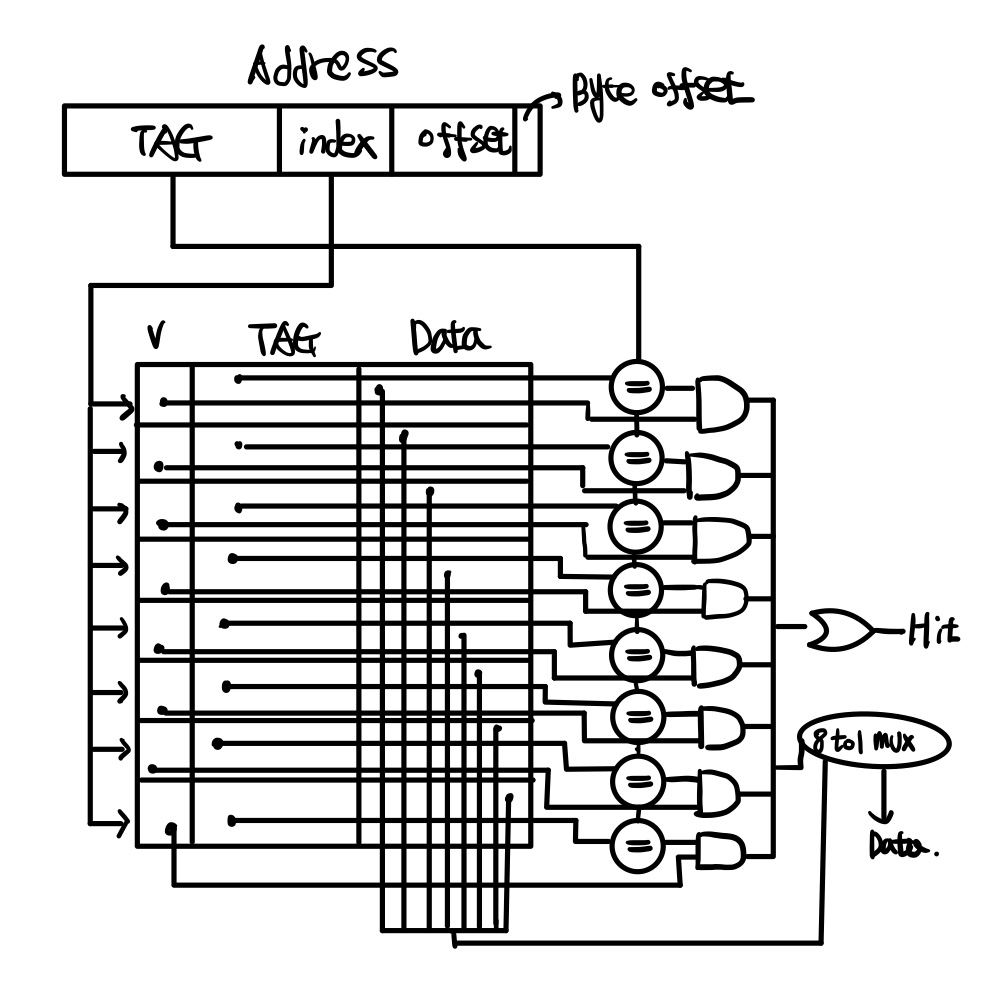
Direct mapped cache와 다를게 없다고 생각하실 수 있지만, Direct mapped cache는 태그를 비교하고 맞는다면 그 Block에
데이터를 저장하지만, Fully associative는 해당하는 모든 Block에 저장할 수 있습니다.
그렇다면 cache의 구조를 감안하면 one-way set associative는 Direct mapped , 8개의 Block이 있다면
Eight-way set associative는 Fully associative가 된다는 것 또한 알 수 있습니다.
Fully associative는 위의 그림과 같이 Block index로 구분되지 않습니다.
왜냐하면 1개의 Block에 Tag와 Data가 붙어있다고 볼 수 있기 때문입니다.

위에 Fully associative의 그림을 비교해보면 구성이 다르게 보이지만 같은 그림이라는 것을 알 수 있습니다.
결론적으로 또 Fully associative의 표를 채우면 아래와 같습니다.
| Cache category | Tag | Block index | Block offset | Byte offset |
| Fully associative | 4bit | X | 2bit | 2bit |
결과적으로 문제의 답을 작성하면 아래와 같게 됩니다.
| Cache category | Tag | Block index | Block offset | Byte offset |
| Direct mapped | 2bit | 2bit | 2bit | 2bit |
| 2-way set associative | 3bit | 1bit | 2bit | 2bit |
| fully associative | 4bit | X | 2bit | 2bit |
결국 n-way set associative는 Direct 구조의 간단한 구조지만 충돌이 많이 발생한다는 단점과
Fully associative 구조의 어느 라인이나 저장될 수 있어서 충돌이 적다는 장점이 있지만
탐색 시간(비용)이 많이 든다는 점을 절충한 구조라고 생각하시면 됩니다.
그리고 위의 cache spec을 가지고 Hit와 Miss를 구분하는 방법은 어떻게 될까요?
| 주소 | Binary | Direct mapped | 2-way set associative | Fully associative | ||||||||||||
| Tag / Block index / Block offset / Hit or Miss / Replace | Tag / Block index / Block offset / Hit or Miss / Replace | Tag / Block index / Block offset / Hit or Miss / Replace | ||||||||||||||
| 0X20 | 0010 0000 | 0 | 2 | 0 | M | - | 1 | 0 | 0 | M | - | 2 | - | 0 | M | - |
| 0XCF | 1100 1111 | 3 | 0 | 2 | M | - | 6 | 0 | 3 | M | - | C | - | 3 | M | - |
| 0X20 | 0010 0000 | 0 | 2 | 0 | H | - | 1 | 0 | 0 | H | - | 2 | - | 0 | H | - |
위의 표에서 보자면, 현재는 cache miss나 hit가 되더라도 Replace가 없는 이유가 있습니다.
다른 예를 들지 않아서 그렇지만, 만약에 더 많은 주소가 들어오게 되면 M일 때, 주소가 Replace됩니다.
현재 제가 예를 든 cache 중에서 Direct mapped로 예를 들자면, Block의 갯수는 총 4개가 있습니다.
만약에 이후에 0X30, 0X40이 들어오게 되면 4개의 Block이 다 차게되어 공간이 없게 됩니다.
여기서 Hit가 아닌 새로운 0X30이 들어오게 되면, 공간이 없기 때문에 Miss가 되고 replace가 일어나게 됩니다.
여기서 사용되는게 LRU(Least Recently Used)알고리즘을 사용하여 replace가 일어나게 됩니다. 물론 다른 알고리즘으로
교체가 일어날 수 있지만, LRU로 예를 들자면 가장 마지막에 사용된 Block이 교체되게 됩니다.
위에서 0X20을 교체할지 0XCF를 교체할지에 대해서 의문이 들지만, LRU에 의하면 0XCF 이후에 0X20이 Hit가 발생했기에
가장 오래 전에 사용된 Block은 0X20이 아닌 0XCF가 되게 됩니다.
교체가 될 때, 0X50으로 교체되고 Replace되는 주소는 0XC0 - 0XCF가 됩니다.
그 이유는 Block은 16Byte이기 때문에 4bit 단위의 주소를 가지게 되고, 교체가 될 때, 4bit 단위로 교체하게 됩니다.
위의 표를 예로 들자면, 0X00 - 0X0F, 0X10 - 0X1F, 0X20 - 0X2F, 0X30 - 0X3F의 사이즈로 Block이 나뉘게 되기 때문입니다.
여기서 0X00 - 0X0F사이에 있는 Data중 하나를 가져오더라도 전체 사이즈대로 다 가져오는 이유는 Locality 때문입니다.
Locality
Locality는 메모리를 어떻게 접근하는지에 대한 패턴을 설명하는 개념으로,
주로 cache memory에서 데이터 접근 효율성을 높이기 위해 활용됩니다.
Locality는 메모리 주소 공간을 효율적으로 사용하는 특성을 의미하며, 메모리 접근 패턴에서 특정 메모리 위치가
일정 시간 동안 빈번하게 참조되거나 인접한 메모리 위치들이 자주 연속적으로 참조되는 경향을 가지게 됩니다.
이 개념을 기반으로 cache는 메모리 접근 성능을 크게 향상시킬 수 있으며, Locality가 높은 경우
cache의 성능을 극대화할 수 있으며, cache hit 확률을 증가시켜 시스템의 전체적인 성능을 향상시키게 됩니다.
Locality는 Temporal Locality(시간 지역성)와 Spatial Locality(공간적 지역성)로 나뉘게 됩니다.
Temporal Locality는 최근에 접근한 데이터가 가까운 미래에도 다시 참조될 가능성이 높다는 특성으로
cache hit율을 증가시키게 되며, 최근에 사용된 데이터는 cache memory에 남게 되어 접근 속도를 향상시킵니다.
Spatial Locality는 한 번 참조된 메모리 주소 근처의 데이터가 곧 참조될 가능성이 높다는 특성입니다.
한 마디로, 한 데이터가 참조되면 이와 인접한 데이터도 곧 참조될 가능성이 크다는 것을 의미하게 되며
연속된 데이터를 cache에 적재하여 후에 참조될 데이터를 빠르게 참조할 수 있게 된다는 것 입니다.
LRU(Least Recently Used), Write Back, Write Through
cache구조와 더불어 간략한 문제를 풀어보며 각 cache 구조에 따라 어떻게 address의 bit가 나뉘는지와
cache에서 hit와 Miss에 따라서 어떻게 교체하는지에 대해서 알아봤습니다.
교체 알고리즘인 LRU를 간단하게 살펴봤는데, LRU 알고리즘은 가장 오랫동안 사용되지 않은 데이터를 교체하는 방식입니다.
즉, 캐시가 가득차서 새로운 데이터를 저장해야 할 때 최근에 사용되지 않은 데이터를 교체하여 새로운 데이터를 cache 적재합니다.
LRU는 Temporal Locality를 기반으로 설계되어 최근에 사용된 데이터는 가까운 미래에 다시 사용될 확률이 높다는 가정으로
오랫동안 사용되지 않은 데이터는 필요하지 않을 가능성이 높으므로 교체하는 것이 효율적이라는 점을 적용한 겁니다.
여기서 Write back고 Write Through는 cache memory에서 데이터를 main memory로 쓰는 방법을 결정하는 방식입니다.
Write through는 데이터가 cache에 쓰일 때 즉시 main memory에도 함께 쓰는 방식으로 cache가 데이터를 변경하면
그 데이터가 동시에 main memory에도 반영되어 두 memory의 데이터가 항상 일관성을 유지하게 됩니다.
하지만 단점으로 cache memory에 바뀐 데이터를 작성하고 main memory에 작성하게 되면서
main memory까지 access time이 오래 걸리기 때문에 이에 해당하는 cost가 많이 든다는 단점이 존재합니다.
그렇다면 Write Back은 어떤 방식일까요?
Write back 방식은 cache에 데이터가 변경되더라도 main memory에 즉시 방연하지 않고,
cache에서 데이터가 교체될 때만 main memory에 쓰는 방식입니다.
그렇다면 하드웨어는 저희와 같이 생각을 하지 못하는데 어떻게 data가 바뀐다는 것을 알 수 있을까요?
write back을 이용하기 위해서 'dirty bit'이라는 bit를 사용하여 cache의 데이터가 바꼈다는 것을 기록하여 알게 됩니다.
cache 내의 데이터가 변경되면 해당 데이터 옆에 dirty bit을 추가하여 cache가 꽉 차거나 해당 데이터가
교체되어 main memory에 가야할 때 dirty bit을 체크하고 dirty bit이 1이라면 해당 데이터도 main memory에 가면서
함께 그 값을 main memory에 쓰는 방식입니다.
해당 방식은 Write through와 같이 데이터가 바뀔 때 마다 main memory에 access하지 않기 때문에
cost가 줄어들게 되고 시스템 성능이 향상하게 됩니다. 하지만 여기에도 단점은 존재하기 마련인데,
구현하기가 복잡하고 cache가 변경될 때 마다 항상 main memory에 쓰지 않기 때문에
동기화되지 않아서 여러 프로세서가 동일한 메모리를 공유하는 환경에서는 데이터 일관성에 대한 문제가 발생할 수 있습니다.
한마디로 잘못된 데이터를 참조할 수 있게 되는 것 입니다.
마지막으로 cache의 성능을 측정하는 방법을 알아보고 마무리 하도록 하겠습니다.
Measuring Cache performance
캐시 성능을 측정하는 방법은 cache hit rate(hit 율), cache miss rate(miss 율), cache access time(access 시간) 그리고
메모리 계층 구조의 대기 시간을 고려한 Average Memory Access Time(AMAT)을 계산하는 방법이 있습니다.
cache hit rate는 cache에 데이터가 있을 때의 비율을 말하는 것입니다.
$\text{Hit rate}\; = \; \frac{\text{cache hit 횟수}}{\text{total memory access 횟수}}$
위와 같은 방식으로 hit rate를 알아낼 수 있습니다. cache hit rate가 높을수록 cache가 데이터를 효율적으로
관리하고 있다는 것을 의미합니다.
cache miss rate는 cache에 데이터가 없어서 main memory에서 데이터를 읽어와야 하는 경우입니다.
cache miss rate는 cache hit rate를 기반으로 아래와 같이 계산됩니다.
$\text{Miss rate} \; = \; \text{1 - Hit rate}$
$\text{Miss rate} \; = \; \frac{\text{cache miss 횟수}}{\text{total memory access 횟수}}$
cache miss rate는 낮을수록 cache가 성능이 좋다는 것을 의미하게 됩니다.
Average Memory Access Time(AMAT)은 cache 성능을 종합적으로 평가하기 위함으로
memory 계층 구조에서 총 memory access time을 계산할 수 있으며 아래와 같습니다.
$\text{AMAT = Hit Time + (Miss rate x Miss penalty)}$
Hit time은 cache hit일 때 데이터를 가져오는데 소요되는 시간입니다. cache access time이라고도 하고
memory보다 빠르기 때문에 보통 매우 짧은 시간이 걸리게 됩니다.
Miss rate는 cache miss rate이고, Miss Penalty는 cache miss가 발생했을 때, main memory에서 데이터를
읽어오는데 걸리는 시간으로 보통 main memory access time으로 cache access time보다 오래걸리게 됩니다.
쉽게 문제로 예를 들어서 적용하자면 다음과 같습니다.
Hit time = 1ns, Miss rate = 5%, Miss penalty = 100ns라면 아래와 같이 계산됩니다.
$\text{AMAT = 1ns + (0.05 x 100ns) = 1ns + 5ns = 6ns}$
위는 평균적으로 memory 접근에 6ns가 소요된다는 것을 의미하게 됩니다.
지금까지 지난 시간에 간단하게 배운 cache에 대해서 문제와 적용방법들을 배우며 자세하게 알아보는 시간을 가지게 되었습니다.
원래는 virtual memory에 대해서도 알아보려고 했지만, 자세하게 보기 위해서 다음 시간에 알아보기로 했습니다.
지금까지 긴 글을 읽어주셔서 감사합니다.
'전자전기공학 > 컴퓨터구조' 카테고리의 다른 글
| [컴퓨터 구조][Parallel] (0) | 2024.11.13 |
|---|---|
| [컴퓨터구조][virtual memory] (10) | 2024.10.27 |
| [컴퓨터구조][Cache] (0) | 2024.10.16 |
| [컴퓨터구조][Hazards #2 Control Hazard] (0) | 2024.10.13 |
| [컴퓨터구조][Hazards #1 Data Hazard] (0) | 2024.10.11 |