[Fundamentals of Electric Circuits #2][회로해석의 기본]

· 목차

   - 노드, 가지, 루프

   - 키르히호프의 법칙

   - 직렬 저항과 전압 분배

   - 병렬 저항과 전류 분배

---

 

앞의 포스팅에서 기본적인 개념에 대해서 배워봤습니다.

회로를 해석하는 방법은 여러가지가 있지만, 회로 해석의 기본에 대해서 배우도록 하겠습니다.

 

---

 

 

노드, 가지, 루프

 

 

 

전기회로의 요소들은 여러 가지 방법으로 연결될 수 있습니다.

앞으로 설명할 개념은 위의 그림을 보면서 읽으시면 이해가 쉬우실거에요.

 

가지는 전압원 또는 저항 등 한 개의 요소를 나타냅니다.

쉽게 이야기해서, 위의 그림에서는 5개의 가지를 가지고 있습니다.

$5v,\; 5\Omega, 2\Omega, 3\Omega, \; 2A$ 등이 가지에 해당합니다.

 

노드는 무엇이 있을까요? 노드는 두 개 또는 그 이상의 가지의 연결점입니다.

노드는 회로에서 한 개의 점으로 표시되며, 두 개의 노드를 연결할 경우에는 두 개의 노드는 한 개의 노드가 됩니다.

이 역시도 위의 그림으로 보자면 a, b, c가 노드가 되는 것을 알 수 있습니다.

두개의 노드를 연결할 경우 두 개의 노드는 한 개의 노드가 된다고 했죠?

위에서 보면 b는 3개의 노드를 합쳐서 b노드가 되는 것이고, c는 4개의 노드가 합쳐져 c노드가 됩니다.

왜 그런지를 직관적으로 알고 싶다면, 오른쪽 그림을 보시면 몇 개의 노드가 어떻게 합쳐지는지 직관적으로 알 수 있습니다.

 

마지막으로, 루프는 무엇일까요? 루프는 회로에서의 모든 폐회로를 말합니다.

모든 노드를 한 번 이상 통과하지 않은 상태로 한 노드에서 시작해서 다시 시작된 노드로 돌아와서 폐경로를 형성합니다.

쉽게 이해하기 위해서 한 번 이상 통과하지 않는다는 전제로 펜을 떼지 않고 선을 쫓아서

시작한 노드로 돌아올 수 있다면 폐루프라고 할 수 있지 않을까요?

 

마지막으로 단일 루프를 가진 네트워크는 네트워크 토폴로지의 근본 법칙을 만족합니다.

$b = l+n-1$

 

 

지금까지 네트워크의 기본 구성 요소에서 대해서 배웠습니다.

토폴로지는 회로의 전압과 전류를 공부하는데 유용한 가치를 가지고 있는데요,

이 부분은 앞으로 전기회로를 공부하는데 기본이 된다고 생각합니다.

 

· 두 개 또는 그 이상의 요소가 직렬연결될 때 그들은 한 개의 노드를 독점적으로 공유해서 결과적으로 같은 전류를 흘려야 한다.

·  두 개 또는 그 이상의 요소가 병렬연결될 때 그들은 같은 두 개의 노드에 연결되어 결과적으로 이들 양단에 같은 전압을 가져야 한다.

 

위의 두 가지 법칙은 앞으로 전기회로를 공부할 때 머릿속에 항상 가지고 있어야 하는 법칙이에요.

쉽게 이야기 하자면, 직렬연결된 요소들은 한 개의 노드를 공유하기 때문에 같은 전류가 흘러야 한다.

병렬연결된 요소는 두 개의 노드에 연결되어 결과적으로 양단에 같은 전압을 가진다는 것 입니다.

직렬연결된 요소 → 같은 전류를 가진다.

병렬연결된 요소 → 같은 전압을 가진다.

 

지금까지 네트워크의 기본적인 요소를 살펴본 만큼, 모든 회로를 해석하는데에 기본적인 법칙이 되기 때문에 항상 머릿속에 있어야 합니다.

만약에, 이 부분을 대충 넘기고 공부신다면 분명히 돌아오게 되기 때문에 반드시 알고 있으셔야 해요.

 

 

 

키르히호프 법칙

 

 

 

키르히호프 법칙은 회로를 해석할 때 옴의 법칙만으로는 회로 해석에 충분하지 않다는 것 입니다.

키르히호프의 첫 번째 법칙은 전류 법칙(KCL)으로 전하 보존 법칙에 기반을 두고 있는데,

이 법칙에 의해서 '시스템 내의 전하의 대수적 합은 변할 수 없다.'는 것 입니다.

이 부분은 앞으로 난해한 모습의 회로를 해석할 때 기본이 되는 법칙이 될 것 입니다.

한 노드에 들어가는 전류와 나오는 전류는 같을 수 밖에없고, 전압 또한 에너지 보존의 법칙에 의해 같을 수 밖에 없다는 것인데,

앞으로 난해한 회로를 해석하다 보면 회로 해석의 방향을 잡는데에 엄청 중요할 거에요.

 

KCL을 설명하는 자료

 

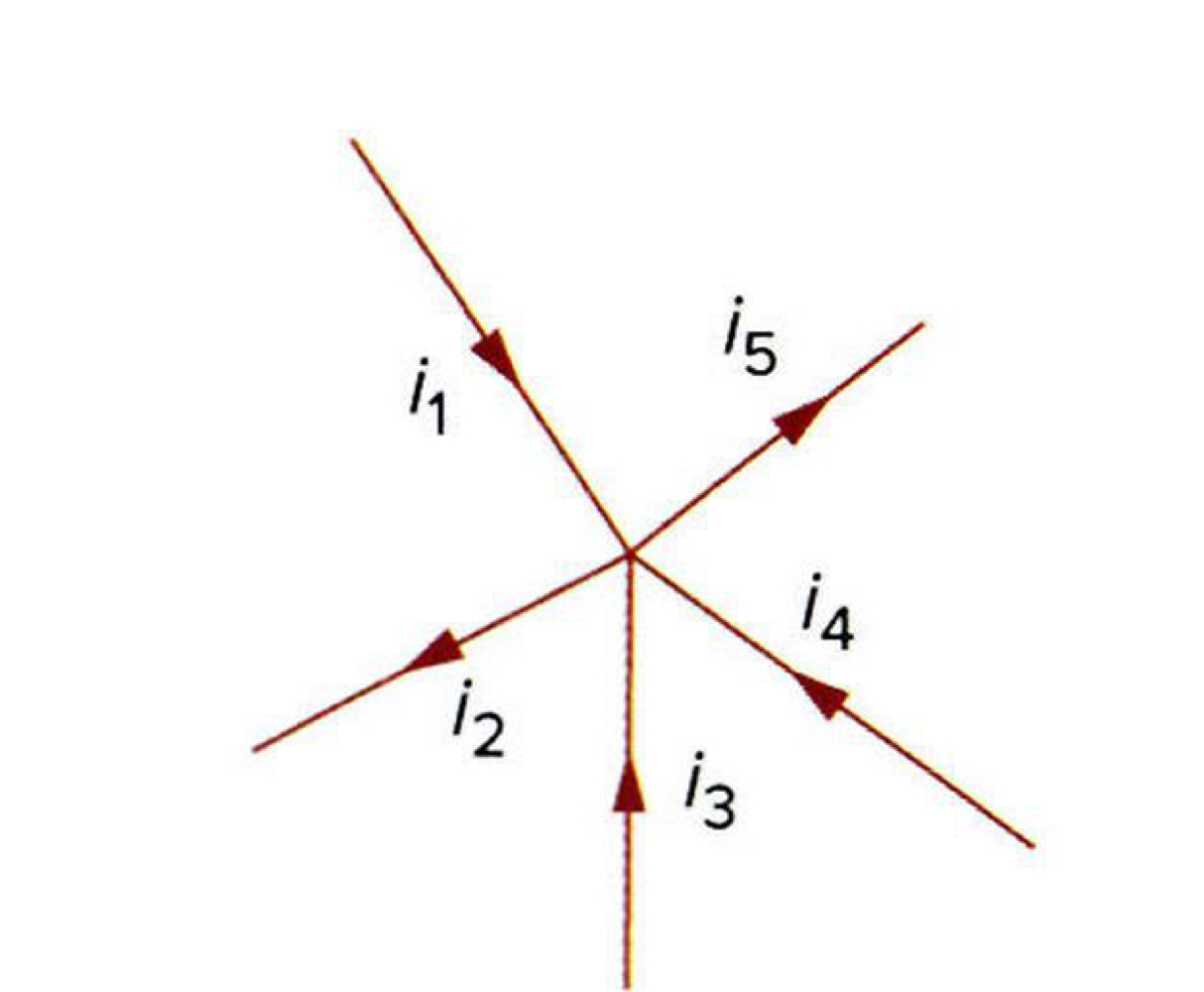
우선 KCL에 대해서 정리하자면, 앞에서 이야기 했듯이 한 개의 노드에 들어오는 전류의 합과

흘러 나가는 전류의 합은 같을 수 밖에 없습니다.

 

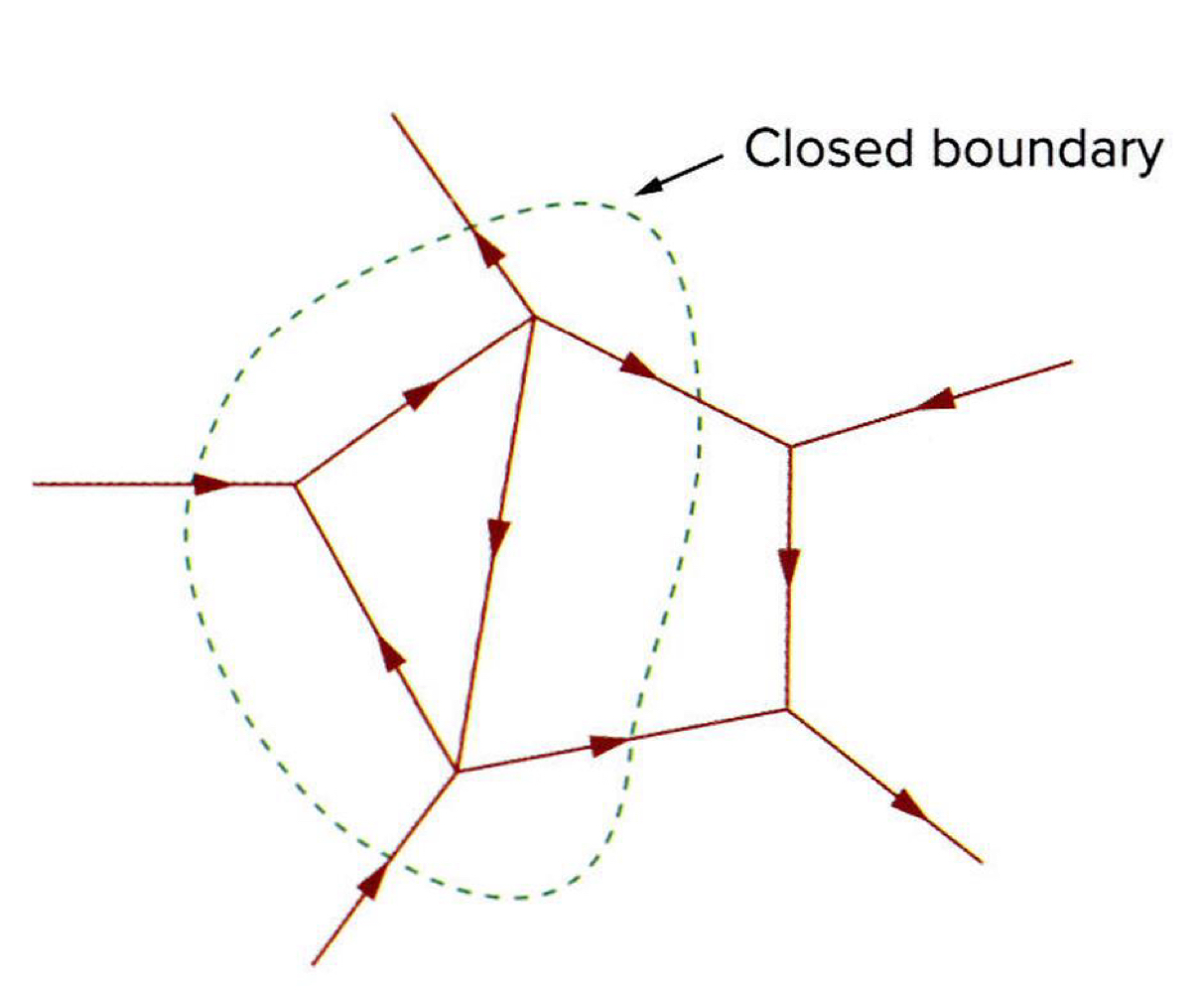
KCL은 또한 한 개의 폐경계 표면에도 적용될 수 있습니다.

오른쪽 그림을 보시면, 한 개의 노드는 닫힌 표면이 한 개의 점으로 줄어든 것으로 볼 수 있기 때문입니다.

정말 난해한 것 같은데,  앞으로 공부를 이어가시다 보면 분명히 모든게 한번에 이해가 되는 시기가 올 거에요.

그리고 분명히 뒤에서 다시 사용될 것 이기 때문에 지금 이해가 되지 않는다고 해도 어렵게 생각하실 필요가 없습니다.

 

개인적인 생각으로, 저 또한 마찬가지였지만, 위의 글을 읽고나면 모든게 이해가 됐다고 생각하실겁니다.

하지만 문제를 풀어보는 순간 모든게 헷갈리실거에요. 그 부분은 문제를 많이 풀다보면 분명히 체화될 거에요.

 

이제 키르히호프의 두 번째 법칙인 전압법칙(KVL)에 대해서 배워보겠습니다.

 

 

 

 

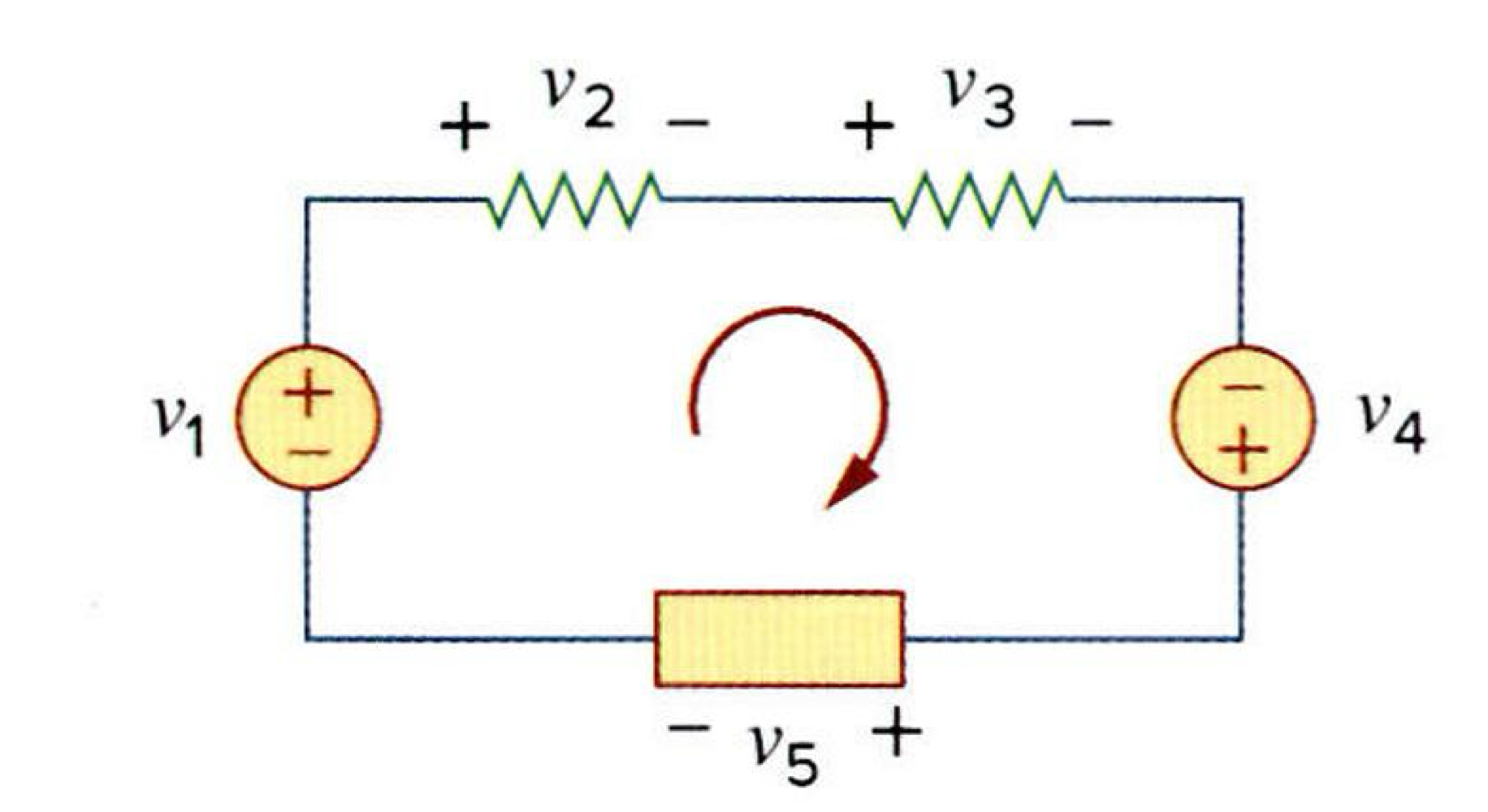
KVL은 에너지 보존 법칙에 기반을 두고 있습니다. 한 개의 폐 경로에서 전압의 대수적인 합은 0인 것을 말합니다.

위의 그림을 보면 루프를 도는 방향을 보실 수 있는데요, 이것은 루프를 돌 때 처음 만나는 단자의 극성입니다.

 

위의 루프에서 KVL을 쓰면 아래와 같이 구할 수 있다는 것을 알 수 있으실거에요.

$-v_{1}+v_{2}+v_{3}-v_{4}+v_{5}=0$

 

항들을 다시 정리하면 아래와 같고,

$v_{2}+v_{3}+v_{5} = v_{1}+v_{4}$

 

정리된 식을 보자면, '전압 강하의 합 = 전압 상승의 합'라는 것을 알 수 있습니다.

 

또한 한 회로에서 KVL을 위배하지 않기 위해서 $v_{1} = v_{2}$가 아니라면,

병렬연결된 두 개의 다른 전압 $v_{1}$과 $v_{2}$가 존재할 수 없다는 것을 아실 수 있습니다.

 

이제 회로를 해석할 때, 옴의 법칙과 키르히호프의 KCL과 KVL법칙을 이용하면 해석을 하기 쉬우실 거에요.

 

그렇다면 저항의 병렬과 직렬 연결된 회로에 대해서 배워보도록 하겠습니다.

회로를 해석하다 보면, 저항을 직렬 또는 병렬로 결합하는 경우가 자주 발생하기 때문에 주의해야 하기 때문에 잘 배우셔야 합니다.

 

 

 

직렬 저항과 전압분배 그리고 병렬 저항과 전류분배

 

 

 

 

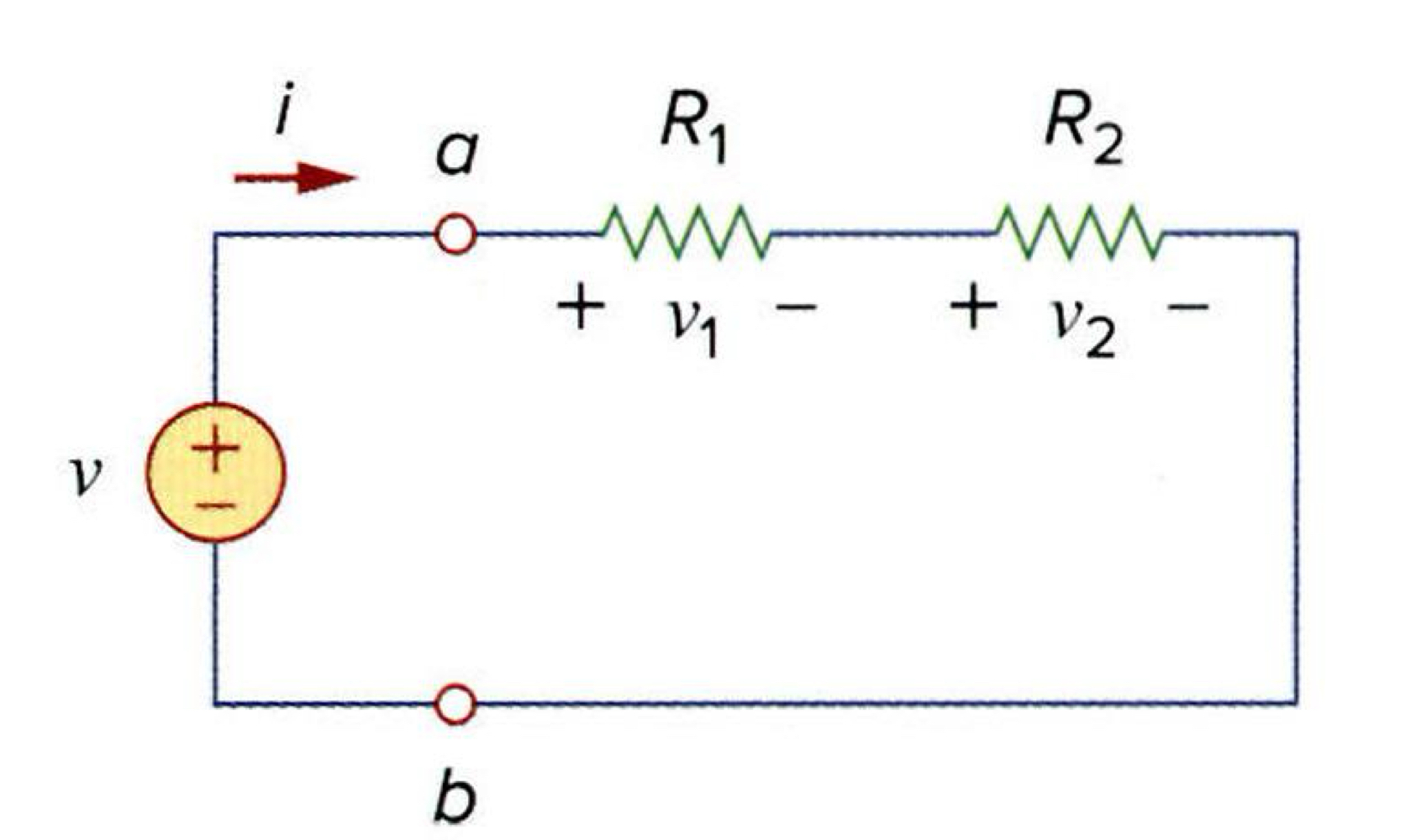
위의 그림을 보게 되면, $R_{1}$과 $R_{2}$ 두 개의 저항은 직렬입니다. 그 이유는 같은 전류가 흐르기 때문입니다.

쉽게 말하자면 같은 전류가 흐른다면 직렬, 같은 전압이 걸리더라도 저항 $R$이 다르다면 전류 $I$가 달라지게 됩니다.

병렬 회로에서는 저항이 작은 경로로 더 많은 전류가 흐르고, 저항이 큰 경로로는 적은 전류가 흐릅니다.

 

이제부터 옴의 법칙과 KVL을 이용해서 전압분배를 사용하는 것은 위의 그림을 통해서 예로 들어보겠습니다.

 

옴의 법칙을 사용하면 $v_{1} = iR_{1}$, $v_{2}=iR_{2}$을 각 저항으로부터 얻을 수 있습니다.

같은 전류가 흐르기 때문에 i가 서로 다르지 않다는 것을 주의하셔야 해요.

 

그리고 위의 루프에서 KVL을 사용하면, $-v+v_{1}+v_{2}=0$임을 알 수 있습니다.

 

위에서 옴의 법칙과 KVL을 통해서 구한 두 식을 조합하면,

$v=v_{1}+v_{2}=i(R_{1}+R_{2})$이고 이를 다시 정리하면,

 

$i=\frac{v}{R_{1}+R_{2}}$입니다.

 

마지막으로, $R_{1}$과 $R_{2}$를 등가저항 $R_{eq}$로 둔다면

 

최종적으로 $v=iR_{eq}$이 됩니다.

 

여기서 등가저항 $R_{eq}$는 두 개의 저항을 한 개의 등가저항으로 둔 것을 의미합니다.

 

등가저항으로 표시하고 난다면, 위의 회로는 아래의 회로와 같이 변경시킬 수 있습니다.

 

 

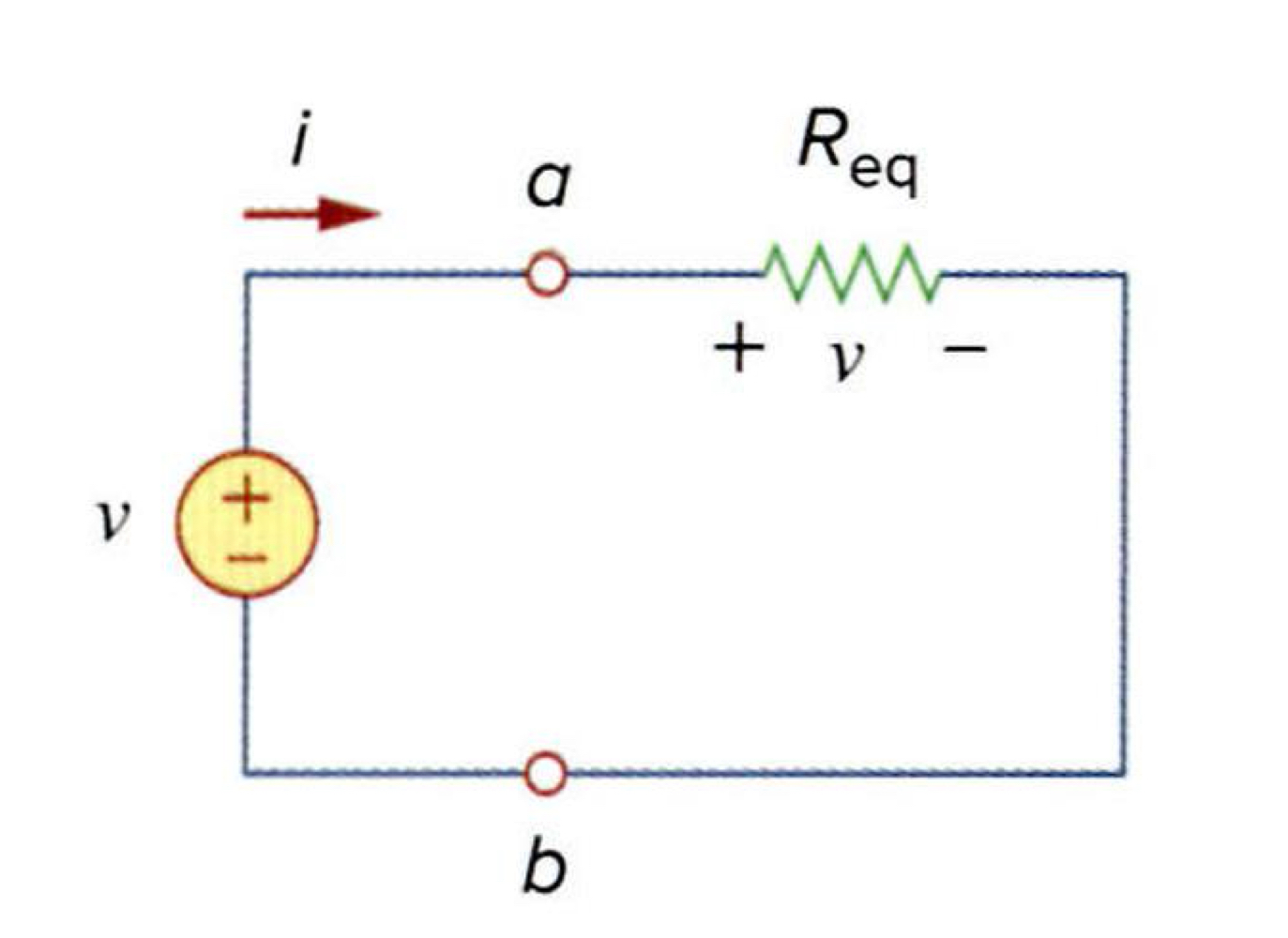
즉, 직렬연결된 저항의 등가저항은 개별 저항의 합과 같습니다.

 

그렇다면 각 저항에 걸리는 전압은 어떻게 구할 수 있을까요?

 

$v_{1} = \frac{R_{1}}{R_{1}+R_{2}}$와 $v_{2} = \frac{R_{2}}{R_{1}+R_{2}}$으로 구할 수 있습니다.

 

위의 전압분배는 첫 번째로 $v = iR_{eq}$으로부터 $v_{1}=iR_{1}$인 옴의 법칙에 대입해서 구한 것임을 알 수 있을거에요.

여기까지 이해하셨다면 $v_{2}$ 또한 전압분배를 썼을 때, 왜 위와 같이 얻어지는지 쉽게 유도하실 수 있으실겁니다.

 

 

이제 병렬저항과 전류분배에 대해서 살펴보도록 하겠습니다.

위에서 간략하게 전압분배를 살펴봤기 때문에 공식을 통해서 전류분배가 어떻게 이뤄지는지 빠르게 살펴보겠습니다.

 

 

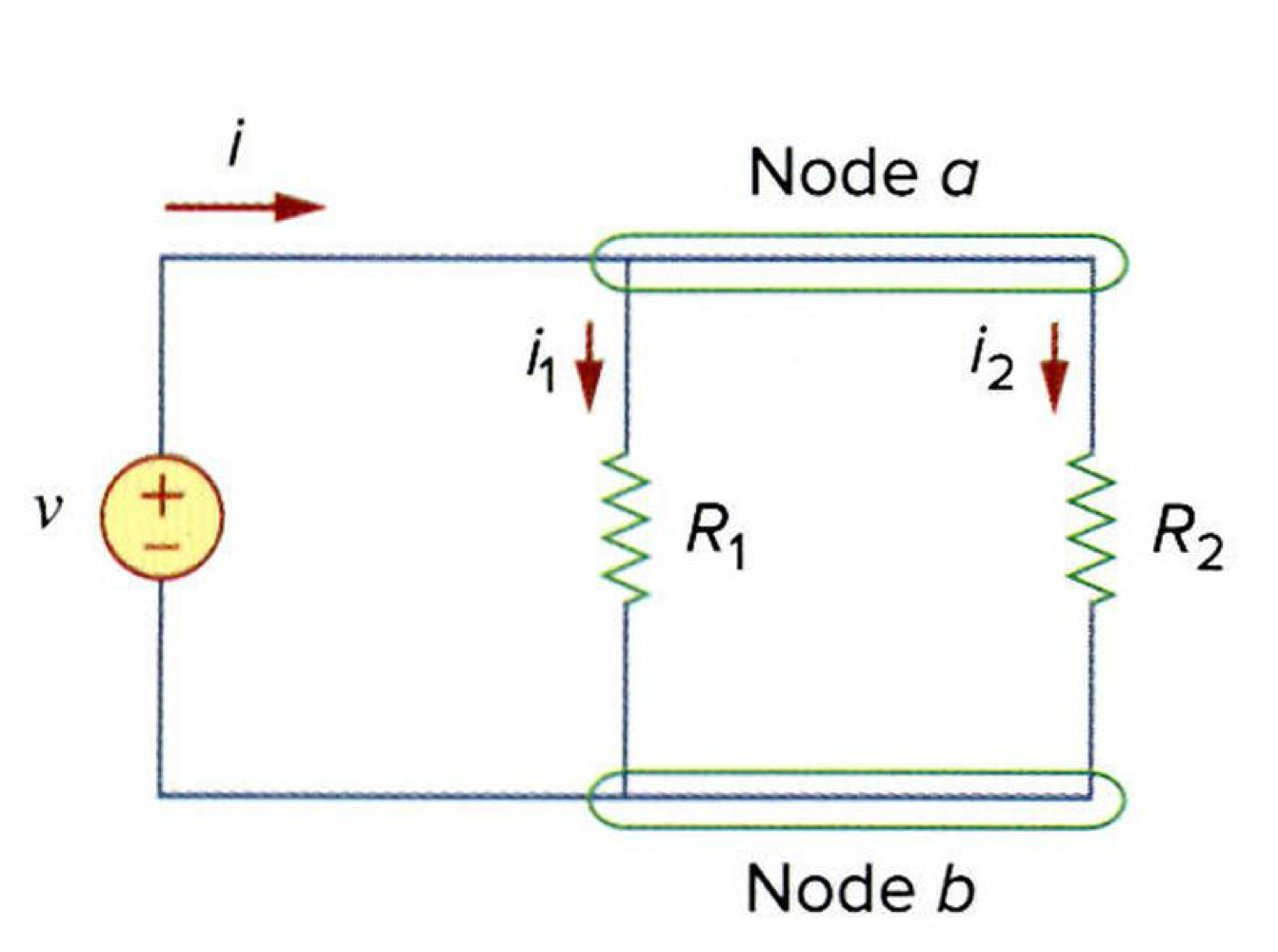
위의 그림에서 각 저항에 옴의 법칙을 사용하게 되면, $v=i_{1}R_{1}=i_{2}R_{2}$임을 알 수 있습니다.

 노드 a에 KCL을 적용하면 전체 전류 i는 $i=i_{1}+i_{2}$입니다.

위의 식을 대입하게 된다면, $i=\frac{v}{R_{1}}+\frac{v}{R_{2}}=v(\frac{1}{R_{1}}+\frac{1}{R_{2}})=\frac{v}{R_{eq}}$로 정리가 됩니다.

 

또한 위의 식에서 $\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}} → \frac{1}{R_{eq}}=\frac{R_{1}+R_{2}}{R_{1}R_{2}}$이 되고, $R_{eq}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}$이 됩니다.

 

쉽게 정리하면, '전류분배의 등가저항은 두 저항의 곱을 두 저항의 합으로 나눈 것과 같다.'라고 할 수 있습니다.

 

또한 등가저항 $R_{eq}$는 병렬연결된 저항 중 가장 작은 저항보다 값이 항상 작습니다.

 

 

이제 연결해서 등가 컨덕턴스와 와이↔델타 변환에 대해서 배우면 기본적인 회로 해석 기본에 대해서 다 배우게 됩니다.

 

그 이후에는 회로 해석 방법을 더 자세히 배우게 될텐데요, Mesh와 Nodal 해석법에 대해서 배우게 되는데요,

오늘은 여기서 끊고 다음 포스팅에서 이어서 해보도록 하겠습니다.

 

 

오늘도 부족한 글을 봐주셔서 감사합니다.

 

다음 포스팅에서 뵙겠습니다!